
【題目】定義:首項為![]() 且公比為正數的等比數列為“
且公比為正數的等比數列為“![]() 數列”.
數列”.
(Ⅰ)已知等比數列![]() (
(![]() )滿足:
)滿足:![]() ,
,![]() ,判斷數列
,判斷數列![]() 是否為“
是否為“![]() 數列”;
數列”;
(Ⅱ)設![]() 為正整數,若存在“
為正整數,若存在“![]() 數列”
數列”![]() (
(![]() ),
),![]() 對任意不大于
對任意不大于![]() 的正整數
的正整數![]() ,都有
,都有![]() 成立,求
成立,求![]() 的最大值.
的最大值.
 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,且過點
,且過點![]() .
.
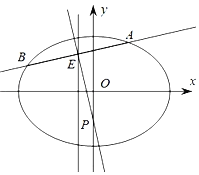
(1)求橢圓C的方程;
(2)直線l交橢圓C于不同的兩點A、B,且![]() 中點E在直線
中點E在直線![]() 上,線段
上,線段![]() 的垂直平分線交y軸于點
的垂直平分線交y軸于點![]() ,求m的取值范圍.
,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】水是生命之源,為了引導市民科學用水,我國加快階梯水價推行,原則是“保基本、建機制、促節約”,其中“保基本”是指保證至少80%的居民用戶用水價格不變,“建機制”是制定合理的階梯用水價格某城市采用簡單隨機抽樣的方法從郊區和城區分別抽取5戶和20戶居民的年人均用水量(單位:噸)進行調研,抽取數據的莖葉圖如下:
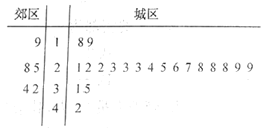
(1)若在郊區的這5戶居民中隨機抽取2戶,求“被抽取的2戶年人均用水量的和超過60噸”的概率;
(2)若該城市郊區和城區的居民戶數比為1:5,現將年人均用水量不超過30噸的用戶定義為第一階梯用戶,只保證這一梯次的居民用戶用水價格不變,試根據樣本估計總體的思想分析此方案是否符合國家“保基本”政策.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《中華人民共和國道路交通安全法》第![]() 條的相關規定:機動車行經人行道時,應當減速慢行;遇行人正在通過人行道,應當停車讓行,俗稱“禮讓斑馬線”《中華人民共和國道路交通安全法》第
條的相關規定:機動車行經人行道時,應當減速慢行;遇行人正在通過人行道,應當停車讓行,俗稱“禮讓斑馬線”《中華人民共和國道路交通安全法》第![]() 條規定:對不禮讓行人的駕駛員處以扣
條規定:對不禮讓行人的駕駛員處以扣![]() 分,罰款
分,罰款![]() 元的處罰.下表是某市一主干路口監控設備所抓拍的
元的處罰.下表是某市一主干路口監控設備所抓拍的![]() 個月內駕駛員不“禮讓斑馬線”行為統計數據:
個月內駕駛員不“禮讓斑馬線”行為統計數據:
月份 |
|
|
|
|
|
不“禮讓斑馬線”駕駛員人數 |
|
|
|
|
|
(1)請利用所給數據求不“禮讓斑馬線”駕駛員人數![]() 與月份
與月份![]() 之間的回歸直線方程
之間的回歸直線方程![]() ,并預測該路口
,并預測該路口![]() 月份的不“禮讓斑馬線”駕駛員人數;
月份的不“禮讓斑馬線”駕駛員人數;
(2)若從表中![]() 月份和
月份和![]() 月份的不“禮讓斑馬線”駕駛員中,采用分層抽樣方法抽取一個容量為
月份的不“禮讓斑馬線”駕駛員中,采用分層抽樣方法抽取一個容量為![]() 的樣本,再從這
的樣本,再從這![]() 人中任選
人中任選![]() 人進行交規調查,求抽到的兩人恰好來自同一月份的概率.
人進行交規調查,求抽到的兩人恰好來自同一月份的概率.
參考公式: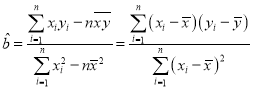 ,
,![]() .
.
參考數據:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國有悠久的金石文化,印信是金石文化的代表之一.印信的形狀多為長方體、正方體或圓柱體,但南北朝時期的官員獨孤信的印信形狀是“半正多面體”(圖1).半正多面體是由兩種或兩種以上的正多邊形圍成的多面體.半正多面體體現了數學的對稱美.圖2是一個棱數為48的半正多面體,它的所有頂點都在同一個正方體的表面上,且此正方體的棱長為1.則該半正多面體共有________個面,其棱長為_________.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩人各進行![]() 次射擊,甲每次擊中目標的概率為
次射擊,甲每次擊中目標的概率為![]() ,乙每次擊中目標的概率
,乙每次擊中目標的概率![]() ,
,
(Ⅰ)記甲擊中目標的次數為![]() ,求
,求![]() 的概率分布及數學期望;
的概率分布及數學期望;
(Ⅱ)求甲恰好比乙多擊中目標![]() 次的概率.
次的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,把邊長為4的正![]() 沿中位線
沿中位線![]() 折起使點
折起使點![]() 到
到![]() 的位置.
的位置.
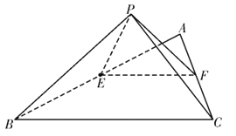
(1)在棱![]() 上是否存在點
上是否存在點![]() ,使得
,使得![]() 平面
平面![]() ?若存在,確定
?若存在,確定![]() 的位置,若不存在,說明理由;
的位置,若不存在,說明理由;
(2)若![]() ,求四棱錐
,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是正方形,
是正方形,![]() 底面
底面![]() ,
,![]() ,點E是
,點E是![]() 的中點,點F在邊
的中點,點F在邊![]() 上移動.
上移動.
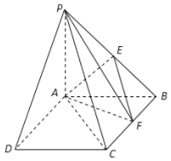
(Ⅰ)若F為![]() 中點,求證:
中點,求證:![]() 平面
平面![]() ;
;
(Ⅱ)求證:![]() ;
;
(Ⅲ)若二面角![]() 的余弦值等于
的余弦值等于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某電子公司新開發一電子產品,該電子產品的一個系統G有3個電子元件組成,各個電子元件能否正常工作的概率均為![]() ,且每個電子元件能否正常工作相互獨立.若系統C中有超過一半的電子元件正常工作,則G可以正常工作,否則就需要維修,且維修所需費用為500元.
,且每個電子元件能否正常工作相互獨立.若系統C中有超過一半的電子元件正常工作,則G可以正常工作,否則就需要維修,且維修所需費用為500元.
(1)求系統不需要維修的概率;
(2)該電子產品共由3個系統G組成,設E為電子產品需要維修的系統所需的費用,求![]() 的分布列與期望;
的分布列與期望;
(3)為提高G系統正常工作概率,在系統內增加兩個功能完全一樣的其他品牌的電子元件,每個新元件正常工作的概率均為![]() ,且新增元件后有超過一半的電子元件正常工作,則C可以正常工作,問:
,且新增元件后有超過一半的電子元件正常工作,則C可以正常工作,問:![]() 滿足什么條件時,可以提高整個G系統的正常工作概率?
滿足什么條件時,可以提高整個G系統的正常工作概率?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com