
【題目】如圖,AB是圓O的直徑,C為圓周上一點,過C作圓O的切線l,過A作直線l的垂線AD,D為垂足,AD與圓O交于點E. 
(1)求證:ABDE=BCCE;
(2)若AB=8,BC=4,求線段AE的長.
【答案】
(1)證明:連接BE,OC,AC,OC∩BE=F,則
∵CD是圓O的切線,
∴OC⊥l,
∵AD⊥l,∴AD∥OC,
∵AB是圓O的直徑,∴AD⊥BE,
∵AD⊥l,∴l(xiāng)∥BE,
∴∠DCE=∠CBE=∠CAB,
∵∠EDC=∠BCA=90°,
∴△EDC∽△BCA,
∴ ![]() =
= ![]() ,
,
∴ABDE=BCCE

(2)解:由(1)可知四邊形EFCD是矩形,
∴DE=CF,
∵圓O的直徑AB=8,BC=4,
∴∠ABC=60°
∴△OBC是等邊三角形,
∴∠EBA=30°,AE=4
【解析】(1)連接BE,OC,OC∩BE=F,證明△EDC∽△BCA,即可證明ABDE=BCCE;(2)證明四邊形EFCD是矩形,△OBC是等邊三角形,即可得出結(jié)論.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=x(1+a|x|),a∈R.
(1)當a=-1時,求函數(shù)![]() 的零點;
的零點;
(2)若函數(shù)f(x)在R上遞增,求實數(shù)a的取值范圍;
(3)設(shè)關(guān)于x的不等式f(x+a)<f(x)的解集為A,若![]() ,求實數(shù)a的取值范圍.
,求實數(shù)a的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為了展示中華漢字的無窮魅力,傳遞傳統(tǒng)文化,提高學(xué)習(xí)熱情,某校開展《中國漢字聽寫大會》的活動.為響應(yīng)學(xué)校號召,2(9)班組建了興趣班,根據(jù)甲、乙兩人近期8次成績畫出莖葉圖,如圖所示,甲的成績中有一個數(shù)的個位數(shù)字模糊,在莖葉圖中用![]() 表示.(把頻率當作概率).
表示.(把頻率當作概率).
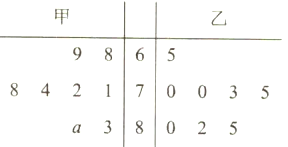
(1)假設(shè)![]() ,現(xiàn)要從甲、乙兩人中選派一人參加比賽,從統(tǒng)計學(xué)的角度,你認為派哪位學(xué)生參加比較合適?
,現(xiàn)要從甲、乙兩人中選派一人參加比賽,從統(tǒng)計學(xué)的角度,你認為派哪位學(xué)生參加比較合適?
(2)假設(shè)數(shù)字![]() 的取值是隨機的,求乙的平均分高于甲的平均分的概率.
的取值是隨機的,求乙的平均分高于甲的平均分的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 為奇函數(shù),
為奇函數(shù), ![]() 為常數(shù).
為常數(shù).
(1)確定![]() 的值;
的值;
(2)求證: ![]() 是
是![]() 上的增函數(shù);
上的增函數(shù);
(3)若對于區(qū)間![]() 上的每一個
上的每一個![]() 值,不等式
值,不等式![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=2x-P2-x,則下列結(jié)論正確的是( )
A. ![]() ,
,![]() 為奇函數(shù)且為R上的減函數(shù)
為奇函數(shù)且為R上的減函數(shù)
B. ![]() ,
,![]() 為偶函數(shù)且為R上的減函數(shù)
為偶函數(shù)且為R上的減函數(shù)
C. ![]() ,
,![]() 為奇函數(shù)且為R上的增函數(shù)
為奇函數(shù)且為R上的增函數(shù)
D. ![]() ,
,![]() 為偶函數(shù)且為R上的增函數(shù)
為偶函數(shù)且為R上的增函數(shù)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c.若sin(A﹣B)+sinC= ![]() sinA.
sinA.
(1)求角B的值;
(2)若b=2,求a2+c2的最大值,并求取得最大值時角A,C的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】給出下列四個命題中:
①命題“若x≥2且y≥3,則x+y≥5”為假命題.
②命題“若x2-4x+3=0,則x=3”的逆否命題為:“若x≠3,則x2-4x+3≠0”.
③“x>1”是“|x|>0”的充分不必要條件
④關(guān)于x的不等式|x+1|+|x-3|≥m的解集為R,則m≤4.
其中所有正確命題的序號是______.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】過橢圓![]() 上一點M作圓
上一點M作圓![]() 的兩條切線,切點為A、B,過A、B的直線與
的兩條切線,切點為A、B,過A、B的直線與![]() 軸和
軸和![]() 軸分別交于
軸分別交于![]() ,則
,則![]() 面積的最小值為( )
面積的最小值為( )
A. ![]() B. 1 C.
B. 1 C. ![]() D.
D. ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com