【題目】已知向量 
=（cosx，﹣ 
）， 
=（ 
sinx，cos2x），x∈R，設函數f（x）= 
．
（1）求f（x）的最小正周期．
（2）求f（x）在[0， 
]上的最大值和最小值．
【答案】
（1）解：函數f（x）= 
=（cosx，﹣ 
）（ 
sinx，cos2x）
= sinxcosx 
=sin（2x﹣ 
）
最小正周期為：T= 
=π．
（2）解：當x∈[0， 
]時，2x﹣ ∈ 
，
由正弦函數y=sinx在 的性質可知，sinx 
，
∴sin（2x﹣ ） ，
∴f（x）∈[﹣ ，1]，
所以函數f（x）在[0， ]上的最大值和最小值分別為：1，﹣ ．
【解析】（1）通過向量的數量積以及二倍角的正弦函數兩角和的正弦函數，化簡函數為一個角的一個三角函數的形式，通過周期公式，求f（x）的最小正周期．（2）通過x在[0， ]，求出f（x）的相位的范圍，利用正弦函數的最值求解所求函數的最大值和最小值．
【考點精析】本題主要考查了兩角和與差的正弦公式和三角函數的最值的相關知識點，需要掌握兩角和與差的正弦公式：
；函數
，當
時，取得最小值為
；當
時，取得最大值為
，則
，
，
才能正確解答此題．
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】在xOy平面上，將兩個半圓弧（x﹣1）2+y2=1（x≥1）和（x﹣3）2+y2=1（x≥3），兩條直線y=1和y=﹣1圍成的封閉圖形記為D，如圖中陰影部分，記D繞y軸旋轉一周而成的幾何體為Ω．過（0，y）（|y|≤1）作Ω的水平截面，所得截面積為4π 
+8π．試利用祖暅原理、一個平放的圓柱和一個長方體，得出Ω的體積值為 ． 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓C： 
(a>b>0)的一個頂點為A(2,0)，離心率為
.直線y＝k(x－1)與橢圓C交于不同的兩點M，N.
(1)求橢圓C的方程；
(2)當△AMN的面積為
時，求k的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在2016年6月英國“脫歐”公投前夕，為了統計該國公民是否有“留歐”意愿，該國某中學數學興趣小組隨機抽查了50名不同年齡層次的公民，調查統計他們是贊成“留歐”還是反對“留歐”．現已得知50人中贊成“留歐”的占60%，統計情況如下表：
年齡層次 | 贊成“留歐” | 反對“留歐” | 合計 |
18歲—19歲 | 6 | ||
50歲及50歲以上 | 10 | ||
合計 | 50 |
（1）請補充完整上述列聯表；
（2）請問是否有97．5%的把握認為贊成“留歐”與年齡層次有關？請說明理由．
參考公式與數據：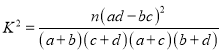
，其中
| 0．15 | 0．10 | 0．05 | 0．025 | 0．010 | 0．005 | 0．001 |
| 2．072 | 2．706 | 3．841 | 5．024 | 6．635 | 7．879 | 10．828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某班運動隊由足球運動員18人，籃球運動員12人、羽毛球運動員6人組成(每人只參加一項)，現從這些運動員中抽取個容量為
的樣本，若分別采用系統抽樣法和分層抽樣法，則都不用剔除個體；當抽取樣本的容量為
時，若采用系統抽樣法，則需要剔除一個個體，則樣本容量
( )
A. 6B. 7C. 12D. 18
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知三棱柱ABC﹣A1B1C1的側棱與底面垂直，體積為 
，底面是邊長為 
的正三角形，若P為底面A1B1C1的中心，則PA與平面A1B1C1所成角的大小為（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=aex，g（x）=lnx-lna，其中a為常數，且曲線y=f（x）在其與y軸的交點處的切線記為l1，曲線y=g（x）在其與x軸的交點處的切線記為l2，且l1∥l2．
（1）求l1，l2之間的距離；
（2）若存在x使不等式
成立，求實數m的取值范圍；
（3）對于函數f（x）和g（x）的公共定義域中的任意實數x0，稱|f（x0）-g（x0）|的值為兩函數在x0處的偏差．求證：函數f（x）和g（x）在其公共定義域內的所有偏差都大于2．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
