
【題目】設a∈R,若不等式![]() 恒成立,則實數a的取值范圍是_____.
恒成立,則實數a的取值范圍是_____.
【答案】[4﹣6![]() ,4+6
,4+6![]() ]
]
【解析】
由題意可得|x3![]() |+|x3
|+|x3![]() |+8≥(4﹣a)x恒成立,討論x>0,x<0,運用基本不等式,可得最值,進而得到所求范圍.
|+8≥(4﹣a)x恒成立,討論x>0,x<0,運用基本不等式,可得最值,進而得到所求范圍.
|x3![]() |+|x3
|+|x3![]() |+ax≥4x﹣8恒成立,
|+ax≥4x﹣8恒成立,
即為|x3![]() |+|x3
|+|x3![]() |+8≥(4﹣a)x恒成立,
|+8≥(4﹣a)x恒成立,
當x>0時,可得4﹣a≤|x2![]() |+|x2
|+|x2![]() |
|![]() 的最小值,
的最小值,
由|x2![]() |+|x2
|+|x2![]() |
|![]() |x2
|x2![]() x2
x2![]() |
|![]() 2x2
2x2![]() 2x2
2x2![]() 3
3![]() 6
6![]() ,
,
當且僅當x3=2即x![]() 取得最小值6
取得最小值6![]() ,即有4﹣a≤6
,即有4﹣a≤6![]() ,則a≥4﹣6
,則a≥4﹣6![]() ;
;
當x<0時,可得4﹣a≥﹣[|x2![]() |+|x2
|+|x2![]() |
|![]() ]的最大值,
]的最大值,
由|x2![]() |+|x2
|+|x2![]() |
|![]() 2x2
2x2![]() 2x2
2x2![]() 3
3![]() 6
6![]() ,
,
當且僅當x3=﹣2即x![]() 取得最大值﹣6
取得最大值﹣6![]() ,即有4﹣a≥﹣6
,即有4﹣a≥﹣6![]() ,則a≤4+6
,則a≤4+6![]() ,
,
綜上可得4﹣6![]() a≤4+6
a≤4+6![]() ,
,
故答案為:[4﹣6![]() ,4+6
,4+6![]() ].
].


科目:高中數學 來源: 題型:
【題目】新高考取消文理科,實行“![]() ”模式,成績由語文、數學、外語統一高考成績和自主選考的3門普通高中學業水平考試等級性考試科目成績構成.為了解各年齡層對新高考的了解情況,隨機調查50人,并把調查結果制成下表:
”模式,成績由語文、數學、外語統一高考成績和自主選考的3門普通高中學業水平考試等級性考試科目成績構成.為了解各年齡層對新高考的了解情況,隨機調查50人,并把調查結果制成下表:
年齡(歲) |
|
|
|
|
|
|
頻數 | 5 | 15 | 10 | 10 | 5 | 5 |
了解 | 4 | 12 | 6 | 5 | 2 | 1 |
(1)把年齡在![]() 稱為中青年,年齡在
稱為中青年,年齡在![]() 稱為中老年,請根據上表完成
稱為中老年,請根據上表完成![]() 列聯表,是否有95%的把握判斷對新高考的了解與年齡(中青年、中老年)有關?
列聯表,是否有95%的把握判斷對新高考的了解與年齡(中青年、中老年)有關?
了解新高考 | 不了解新高考 | 總計 | |
中青年 | |||
中老年 | |||
總計 |
附: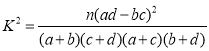 .
.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
(2)若從年齡在![]() 的被調查者中隨機選取3人進行調查,記選中的3人中了解新高考的人數為
的被調查者中隨機選取3人進行調查,記選中的3人中了解新高考的人數為![]() ,求
,求![]() 的分布列以及
的分布列以及![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為等差數列,各項為正的等比數列
為等差數列,各項為正的等比數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,
,![]() ,__________.在①
,__________.在①![]() ;②
;②![]() ;③
;③![]() 這三個條件中任選其中一個,補充在橫線上,并完成下面問題的解答(如果選擇多個條件解答,則以選擇第一個解答記分).
這三個條件中任選其中一個,補充在橫線上,并完成下面問題的解答(如果選擇多個條件解答,則以選擇第一個解答記分).
(1)求數列![]() 和
和![]() 的通項公式;
的通項公式;
(2)求數列![]() 的前
的前![]() 項和
項和![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() 、
、![]() ,
,![]() ,點A為橢圓C上異于左右頂點的任意一點,A關于原點O的對稱點為B,
,點A為橢圓C上異于左右頂點的任意一點,A關于原點O的對稱點為B,![]() ,且
,且![]() .
.
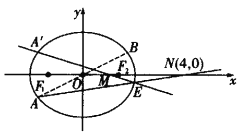
(Ⅰ)求橢圓C的標準方程;
(Ⅱ)若![]() 是A關于x軸的對稱點,設點
是A關于x軸的對稱點,設點![]() ,連接NA,直線NA與橢圓C相交于點E,直線
,連接NA,直線NA與橢圓C相交于點E,直線![]() 與x軸相交于點M,求點M的坐標.
與x軸相交于點M,求點M的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某國營企業集團公司現有員工1000名,平均每人每年創造利潤10萬元.為了激化內部活力,增強企業競爭力,集團公司董事會決定優化產業結構,調整出![]() (
(![]() )名員工從事第三產業;調整后,他們平均每人每年創造利潤
)名員工從事第三產業;調整后,他們平均每人每年創造利潤![]() 萬元
萬元![]() ,剩下的員工平均每人每年創造的利潤可以提高
,剩下的員工平均每人每年創造的利潤可以提高![]() %.
%.
(Ⅰ)若要保證剩余員工創造的年總利潤不低于原來1000名員工創造的年總利潤,則最多調整出多少名員工從事第三產業?
(Ⅱ)在(1)的條件下,若調整出的員工創造的年總利潤始終不高于剩余員工創造的年總利潤,則實數![]() 的取值范圍是多少?
的取值范圍是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】圓![]() :
:![]() (
(![]() )過點
)過點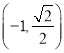 ,離心率為
,離心率為![]() ,其左、右焦點分別為
,其左、右焦點分別為![]() ,
,![]() ,且過焦點
,且過焦點![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() ,
,![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)若點![]() 的坐標為
的坐標為![]() ,設直線
,設直線![]() 與直線
與直線![]() 的斜率分別為
的斜率分別為![]() ,試證明:
,試證明:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com