
對于函數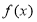 ,若存在實數對(
,若存在實數對(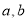 ),使得等式
),使得等式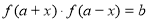 對定義域中的每一個
對定義域中的每一個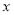 都成立,則稱函數
都成立,則稱函數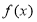 是“(
是“(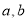 )型函數”.
)型函數”.
(Ⅰ)判斷函數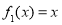 是否為 “(
是否為 “(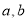 )型函數”,并說明理由;
)型函數”,并說明理由;
(Ⅱ)若函數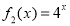 是“(
是“(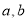 )型函數”,求出滿足條件的一組實數對
)型函數”,求出滿足條件的一組實數對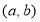 ;,
;,
(Ⅲ)已知函數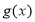 是“(
是“(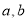 )型函數”,對應的實數對
)型函數”,對應的實數對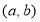 為
為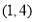 .當
.當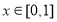 時,
時,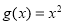
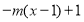
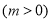 ,若當
,若當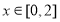 時,都有
時,都有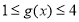 ,試求
,試求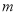 的取值范圍.
的取值范圍.
(Ⅰ)詳見解析;(Ⅱ) (答案還有其他可能);(Ⅲ)
(答案還有其他可能);(Ⅲ)
【解析】
試題分析:(Ⅰ) 由給出的定義可知 展開后的方程中如果不含x說明對任意x都成立,則函數
展開后的方程中如果不含x說明對任意x都成立,則函數 是“(
是“( )型函數” ,如果展開后的方程含x,則根據方程只能求出某個或某些x滿足要求而不是每一個x都符合,則函數
)型函數” ,如果展開后的方程含x,則根據方程只能求出某個或某些x滿足要求而不是每一個x都符合,則函數 不是“(
不是“( )型函數(Ⅱ)根據定義列出方程 ,滿足方程的實數對應有無數對,只取其中一對就可以(Ⅲ)難度系數較大,應先根據題意分析出當
)型函數(Ⅱ)根據定義列出方程 ,滿足方程的實數對應有無數對,只取其中一對就可以(Ⅲ)難度系數較大,應先根據題意分析出當 時,
時,  ,此時
,此時  。根據已知
。根據已知 時,
時, ,其對稱軸方程為
,其對稱軸方程為 。屬動軸定區間問題需分類討論,在每類中得出
。屬動軸定區間問題需分類討論,在每類中得出 時
時 的值域即
的值域即 的值域,從而得出
的值域,從而得出 時
時 的值域,把兩個值域取并集即為
的值域,把兩個值域取并集即為 的
的 的值域,由
的值域,由 可知
可知 的值域是
的值域是 的子集,列出關于m的不等式即可求解。
的子集,列出關于m的不等式即可求解。
試題解析:(1) 不是“(
不是“( )型函數”,因為不存在實數對
)型函數”,因為不存在實數對 使得
使得 ,
,
即 對定義域中的每一個
對定義域中的每一個 都成立;
都成立;
(2)由 ,得
,得 ,所以存在實數對,
,所以存在實數對,
如 ,使得
,使得 對任意的
對任意的 都成立;
都成立;
(3)由題意得, ,所以當
,所以當 時,
時,  ,其中
,其中 ,而
,而 時,
時, ,其對稱軸方程為
,其對稱軸方程為 .
.
當 ,即
,即 時,
時, 在
在 上的值域為
上的值域為 ,即
,即 ,則
,則 在
在 上的值域為
上的值域為 ,由題意得
,由題意得 ,從而
,從而 ;
;
當 ,即
,即 時,
時, 的值域為
的值域為 ,即
,即 ,則
,則 在
在 上的值域為
上的值域為 ,則由題意,得
,則由題意,得 且
且 ,解得
,解得 ;
;
當 ,即
,即 時,
時, 的值域為
的值域為 ,即
,即 ,則
,則 在
在 上的值域為
上的值域為 ,即
,即 ,則
,則 ,解得
,解得 .
.
綜上所述,所求 的取值范圍是
的取值范圍是 .
.
考點:對新概念的理解能力,以及動軸定區間求二次函數的值域問題。


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:高中數學 來源:2016屆江西新余市高一上學期期末質量檢測數學試卷(解析版) 題型:選擇題
已知函數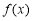 是定義在R上的偶函數,且在區間
是定義在R上的偶函數,且在區間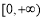 單調遞增. 若實數
單調遞增. 若實數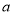 滿足
滿足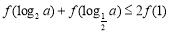 , 則
, 則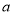 的取值范圍是( )
的取值范圍是( )
A. 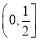 B.
B. 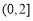 C.
C. 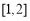 D.
D. 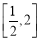
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com