
【題目】已知四棱錐P﹣ABCD中,側面PAD⊥底面ABCD,∠BAD=60°,△PAD是邊長為2的正三角形,底面ABCD是菱形,點M為PC的中點.
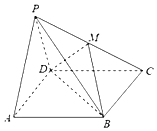
(1)求證:PA∥平面MDB;
(2)求三棱錐A﹣BDM的體積.
【答案】(1)證明見解析;(2)![]()
【解析】
(1)連結AC,交BD于O,連結OM,推導出OM∥PA,由此能證明PA∥平面MDB.
(2)三棱錐A﹣BDM的體積VA﹣BDM=VM﹣ABD,由此能求出結果.
(1)證明:連結AC,交BD于O,連結OM,如圖:
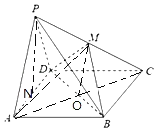
∵底面ABCD是菱形,∴O是AC中點,
∵點M為PC的中點.∴OM∥PA,
∵![]() 平面BDM,
平面BDM,![]() 平面BDM,
平面BDM,
∴PA∥平面MDB.
(2)取AD中點N,連結PN,
∵四棱錐P﹣ABCD中,側面PAD⊥底面ABCD,∠BAD=60°,
△PAD是邊長為2的正三角形,底面ABCD是菱形,點M為PC的中點,
∴PN⊥平面ABCD,PN![]() ,
,
M到平面ABD的距離d![]() ,
,
S△ABD![]() ,
,
∴三棱錐A﹣BDM的體積為:VA﹣BDM=VM﹣ABD![]() .
.


 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案科目:高中數學 來源: 題型:
【題目】個人所得稅是國家對本國公民、居住在本國境內的個人的所得和境外個人來源于本國的所得征收的一種所得稅.我國在1980年9月10日,第五屆全國人民代表大會第三次會議通過并公布了《中華人民共和國個人所得稅法》.公民依法誠信納稅是義務,更是責任現將自2013年至2017年的個人所得稅收入統計如下

并制作了時間代號x與個人所得稅收入的如如圖所示的散點圖:
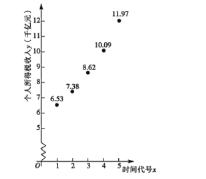
根據散點圖判斷,可用①y=menx與②![]() 作為年個人所得稅收入y關于時間代號x的回歸方程,經過數據運算和處理,得到如下數據:
作為年個人所得稅收入y關于時間代號x的回歸方程,經過數據運算和處理,得到如下數據:

以下計算過程中四舍五入保留兩位小數.
(1)根據所給數據,分別求出①,②中y關于x的回歸方程;
(2)已知2018年個人所得稅收人為13.87千億元,用2018年的數據驗證(1)中所得兩個回歸方程,哪個更適宜作為y關于時間代號x的回歸方程?
(3)你還能從統計學哪些角度來進一步確認哪個回歸方程更適宜? (只需敘述,不必計算)
附:對于一組數據![]() 其回歸直線
其回歸直線![]() 的斜率和截距的最小二乘估計分別為:
的斜率和截距的最小二乘估計分別為: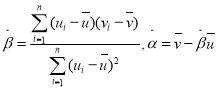
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數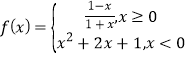 ,函數g(x)=f(1-x)-kx+k-
,函數g(x)=f(1-x)-kx+k-![]() 恰有三個不同的零點,則k的取值范圍是( )
恰有三個不同的零點,則k的取值范圍是( )
A. (-2-![]() ,0]∪
,0]∪![]() B. (-2+
B. (-2+![]() ,0]∪
,0]∪![]()
C. (-2-![]() ,0]∪
,0]∪![]() D. (-2+
D. (-2+![]() ,0]∪
,0]∪![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,
,![]() ,
,![]() 分別為
分別為![]() 的中點,
的中點,![]() ,將
,將![]() 沿
沿![]() 折起,得到四棱錐
折起,得到四棱錐![]() ,
,![]() 為
為![]() 的中點.
的中點.
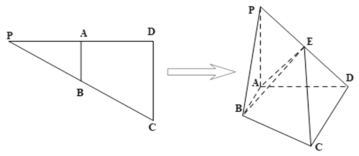
(1)證明:![]() 平面
平面![]() ;
;
(2)當正視圖方向與向量![]() 的方向相同時,此時
的方向相同時,此時![]() 的正視圖的面積為
的正視圖的面積為![]() ,求四棱錐
,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
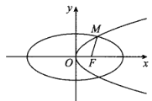
【題目】如圖,已知橢圓![]() 的右焦點F為拋物線
的右焦點F為拋物線![]() 的焦點,點M為
的焦點,點M為![]() 和
和![]() 在第一象限的交點,且
在第一象限的交點,且![]() .
.
(Ⅰ)求拋物線![]() 的標準方程;
的標準方程;
(Ⅱ)若![]() ,過焦點F的直線l與
,過焦點F的直線l與![]() 相交于A,B兩點,已知
相交于A,B兩點,已知![]() ,求
,求![]() 取得最大值時直線l的方程.
取得最大值時直線l的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點O為坐標原點,橢圓C:![]() (a>b>0)的左、右焦點分別為F1,F2,離心率為
(a>b>0)的左、右焦點分別為F1,F2,離心率為![]() ,點I,J分別是橢圓C的右頂點、上頂點,△IOJ的邊IJ上的中線長為
,點I,J分別是橢圓C的右頂點、上頂點,△IOJ的邊IJ上的中線長為![]() .
.
(1)求橢圓C的標準方程;
(2)過點H(-2,0)的直線交橢圓C于A,B兩點,若AF1⊥BF1,求直線AB的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2018年9月24日,阿貝爾獎和菲爾茲獎雙料得主、英國著名數學家阿蒂亞爵士宣布自己證明了黎曼猜想,這一事件引起了數學界的震動,在1859年,德國數學家黎曼向科學院提交了題目為《論小于某值的素數個數》的論文并提出了一個命題,也就是著名的黎曼猜想.在此之前,著名數學家歐拉也曾研究過這個問題,并得到小于數字![]() 的素數個數大約可以表示為
的素數個數大約可以表示為![]() 的結論(素數即質數,
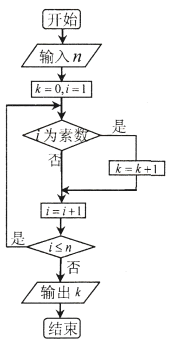
的結論(素數即質數,![]() ).根據歐拉得出的結論,如下流程圖中若輸入
).根據歐拉得出的結論,如下流程圖中若輸入![]() 的值為
的值為![]() ,則輸出
,則輸出![]() 的值應屬于區間( )
的值應屬于區間( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com