Question

已知z="2x" +y，x，y滿足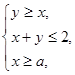且z的最大值是最小值的4倍，則a的值是      ．

Answer 1

解析試題分析：題意可得先作出不等式表示的 平面區域，由z=2x+y可得y=-2x+z，則z表示直線y=-2x+z在y軸上的截距，截距越大，z越大，可求Z的最大值與最小值，即可求解a
由題意可得，B（1，1）
∴a＜1，不等式組表示的 平面區域如圖所示的△ABC
由z=2x+y可得y=-2x+z，則z表示直線y=-2x+z在y軸上的截距，截距越大，z越大
作直線L：y=-2x，把直線向可行域平移，當直線經過C時Z最小，當直線經過點B時，Z最大，由x=a,y=x，解得交點（a,a），此時Z=3a
由y=x,x+y-2=0,可得交點為B（1，1），此時z=3，故可知∴3=4×3a
∴a=故答案
考點：線性規劃的最優解問題
點評：線性規劃是高考重要內容，也是常考內容．此題考查該知識點增加一點變化，比較好．