
某公司試銷一種成本單價(jià)為500元/件的新產(chǎn)品,規(guī)定試銷時(shí)銷售單價(jià)不低于成本單價(jià),又不高于800元/件.經(jīng)試銷調(diào)查,發(fā)現(xiàn)銷售量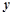 (件)與銷售單價(jià)
(件)與銷售單價(jià)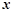 (元/件)可近似看作一次函數(shù)
(元/件)可近似看作一次函數(shù)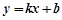 的關(guān)系(如圖所示).
的關(guān)系(如圖所示). 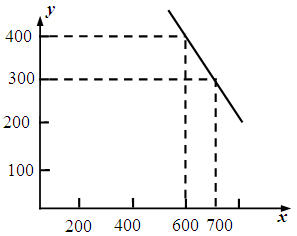
(1)根據(jù)圖象,求一次函數(shù)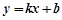 的表達(dá)式;
的表達(dá)式;
(2)設(shè)公司獲得的毛利潤(毛利潤=銷售總價(jià)—成本總價(jià))為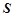 元. 試用銷售單價(jià)
元. 試用銷售單價(jià)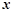 表示毛利潤
表示毛利潤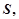 并求銷售單價(jià)定為多少時(shí),該公司獲得最大毛利潤?最大毛利潤是多少?此時(shí)的銷售量是多少?
并求銷售單價(jià)定為多少時(shí),該公司獲得最大毛利潤?最大毛利潤是多少?此時(shí)的銷售量是多少?
(1)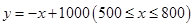 ;(2)當(dāng)
;(2)當(dāng)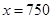 時(shí),
時(shí),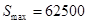 ,此時(shí)
,此時(shí)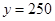 .
.
解析試題分析:(1)由于為一次函數(shù)所以只需從圖中找兩點(diǎn)坐標(biāo)代入即可;(2)銷售總價(jià)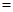 銷售單價(jià)
銷售單價(jià) 銷售量,成本總價(jià)
銷售量,成本總價(jià)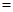 成本單價(jià)
成本單價(jià) 銷售量,得毛利潤
銷售量,得毛利潤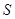 為關(guān)于
為關(guān)于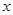 的一元二次函數(shù)注意
的一元二次函數(shù)注意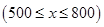 ,為二次函數(shù)給定區(qū)間求最值問題.
,為二次函數(shù)給定區(qū)間求最值問題.
試題解析:⑴由圖象知,當(dāng)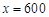 時(shí),
時(shí),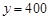 ;當(dāng)
;當(dāng)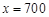 時(shí),
時(shí),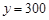 ,
,
分別代入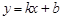 ,解得
,解得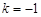 ,
, ,
,
所以 . 6分
. 6分
⑵銷售總價(jià)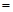 銷售單價(jià)
銷售單價(jià)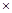 銷售量
銷售量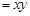 ,成本總價(jià)
,成本總價(jià)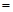 成本單價(jià)
成本單價(jià)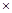 銷售量
銷售量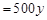 ,
,
代入求毛利潤的公式,得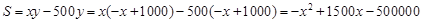 10分
10分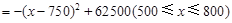 ,
,
當(dāng)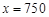 時(shí),
時(shí), ,此時(shí)
,此時(shí) . 14分
. 14分
答:當(dāng)銷售單價(jià)為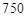 元/件時(shí),可獲得最大毛利潤為
元/件時(shí),可獲得最大毛利潤為 元,此時(shí)銷售量為
元,此時(shí)銷售量為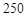 件. 16分
件. 16分
考點(diǎn):1.函數(shù)的實(shí)際應(yīng)用問題;2.二次函數(shù)求最值.


 全能練考卷系列答案
全能練考卷系列答案 一課一練課時(shí)達(dá)標(biāo)系列答案
一課一練課時(shí)達(dá)標(biāo)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
某公司生產(chǎn)一種電子儀器的固定成本為20000元,每生產(chǎn)一臺儀器需增加投入100元,已知總收益滿足函數(shù):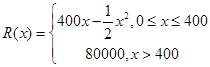 ,其中
,其中 是儀器的月產(chǎn)量.
是儀器的月產(chǎn)量.
(注:總收益=總成本+利潤)
(1)將利潤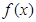 表示為月產(chǎn)量
表示為月產(chǎn)量 的函數(shù);
的函數(shù);
(2)當(dāng)月產(chǎn)量 為何值時(shí),公司所獲利潤最大?最大利潤為多少元?
為何值時(shí),公司所獲利潤最大?最大利潤為多少元?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某興趣小組要測量電視塔AE的高度H(單位:m).如示意圖,垂直放置的標(biāo)桿BC的高度h=4 m,仰角∠ABE=α,∠ADE=β.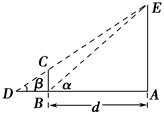
(1)該小組已測得一組α,β的值,算出了tan α=1.24,tan β=1.20,請據(jù)此算出H的值;
(2)該小組分析若干測得的數(shù)據(jù)后,認(rèn)為適當(dāng)調(diào)整標(biāo)桿到電視塔的距離d(單位:m),使α與β之差較大,可以提高測量精度.若電視塔的實(shí)際高度為125 m,試問d為多少時(shí),α-β最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知函數(shù)f(x)= ,x∈[-1,1],函數(shù)g(x)=[f(x)]2-2af(x)+3的最小值為h(a).
,x∈[-1,1],函數(shù)g(x)=[f(x)]2-2af(x)+3的最小值為h(a).
(1)求h(a);
(2)是否存在實(shí)數(shù)m、n同時(shí)滿足下列條件:
①m>n>3;
②當(dāng)h(a)的定義域?yàn)閇n,m]時(shí),值域?yàn)閇n2,m2]?若存在,求出m、n的值;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某村莊擬修建一個(gè)無蓋的圓柱形蓄水池(不計(jì)厚度).設(shè)該蓄水池的底面半徑為r米,高為h米,體積為V立方米.假設(shè)建造成本僅與表面積有關(guān),側(cè)面積的建造成本為100元/平方米,底面的建造成本為160元/平方米,該蓄水池的總建造成本為12 000π元(π為圓周率).
(1)將V表示成r的函數(shù)V(r),并求該函數(shù)的定義域;
(2)討論函數(shù)V(r)的單調(diào)性,并確定r和h為何值時(shí)該蓄水池的體積最大.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
若函數(shù)f(x)對任意的實(shí)數(shù)x1,x2∈D,均有|f(x2)-f(x1)|≤|x2-x1|,則稱函數(shù)f(x)是區(qū)間D上的“平緩函數(shù)”.
(1)判斷g(x)=sin x和h(x)=x2-x是不是實(shí)數(shù)集R上的“平緩函數(shù)”,并說明理由;
(2)若數(shù)列{xn}對所有的正整數(shù)n都有|xn+1-xn|≤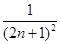 ,設(shè)yn=sin xn,求證:|yn+1-y1|<
,設(shè)yn=sin xn,求證:|yn+1-y1|< .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某市對排污水進(jìn)行綜合治理,征收污水處理費(fèi),系統(tǒng)對各廠一個(gè)月內(nèi)排出的污水量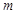 噸收取的污水處理費(fèi)
噸收取的污水處理費(fèi)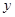 元,運(yùn)行程序如下所示:請寫出y與m的函數(shù)關(guān)系,并求排放污水150噸的污水處理費(fèi)用.
元,運(yùn)行程序如下所示:請寫出y與m的函數(shù)關(guān)系,并求排放污水150噸的污水處理費(fèi)用.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
某單位擬建一個(gè)扇環(huán)面形狀的花壇(如圖所示),該扇環(huán)面是由以點(diǎn)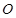 為圓心的兩個(gè)同心圓弧和延長后通過點(diǎn)
為圓心的兩個(gè)同心圓弧和延長后通過點(diǎn)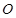 的兩條直線段圍成.按設(shè)計(jì)要求扇環(huán)面的周長為30米,其中大圓弧所在圓的半徑為10米.設(shè)小圓弧所在圓的半徑為
的兩條直線段圍成.按設(shè)計(jì)要求扇環(huán)面的周長為30米,其中大圓弧所在圓的半徑為10米.設(shè)小圓弧所在圓的半徑為 米,圓心角為
米,圓心角為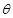 (弧度).
(弧度).
(1)求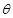 關(guān)于
關(guān)于 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)已知在花壇的邊緣(實(shí)線部分)進(jìn)行裝飾時(shí),直線部分的裝飾費(fèi)用為4元/米,弧線部分的裝飾費(fèi)用為9元/米.設(shè)花壇的面積與裝飾總費(fèi)用的比為 ,求
,求 關(guān)于
關(guān)于 的函數(shù)關(guān)系式,并求出
的函數(shù)關(guān)系式,并求出 為何值時(shí),
為何值時(shí), 取得最大值?
取得最大值?
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com