
【題目】某中學(xué)組織了地理知識(shí)競(jìng)賽,從參加考試的學(xué)生中抽出40名學(xué)生,將其成績(jī)(均為整數(shù))分成六組![]() ,
,![]() ,…,
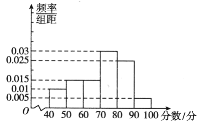
,…,![]() ,其部分頻率分布直方圖如圖所示.觀察圖形,回答下列問(wèn)題.
,其部分頻率分布直方圖如圖所示.觀察圖形,回答下列問(wèn)題.

(1)求成績(jī)?cè)?/span>![]() 的頻率,并補(bǔ)全這個(gè)頻率分布直方圖:
的頻率,并補(bǔ)全這個(gè)頻率分布直方圖:
(2)估計(jì)這次考試的及格率(60分及以上為及格)和平均分;(計(jì)算時(shí)可以用組中值代替各組數(shù)據(jù)的平均值)
(3)從成績(jī)?cè)?/span>![]() 和
和![]() 的學(xué)生中選兩人,求他們?cè)谕环謹(jǐn)?shù)段的概率.
的學(xué)生中選兩人,求他們?cè)谕环謹(jǐn)?shù)段的概率.
【答案】(1)0.3
(2)75%;71
(3)![]()
【解析】
根據(jù)各組的頻率之和等于1,即可得出成績(jī)?cè)?/span>![]() 的頻率。
的頻率。
根據(jù)題意,計(jì)算出![]() ,
,![]() ,
,![]() ,
,![]() 這四個(gè)組頻率之和即可估計(jì)出本次考試的及格率;利用每組組中值乘該組的頻率再求和 即可得出本次考試的平均分。
這四個(gè)組頻率之和即可估計(jì)出本次考試的及格率;利用每組組中值乘該組的頻率再求和 即可得出本次考試的平均分。
成績(jī)?cè)?/span>![]() 的人數(shù)為4人,成績(jī)?cè)?/span>
的人數(shù)為4人,成績(jī)?cè)?/span>![]() 的人數(shù)為2人,從成績(jī)?cè)?/span>
的人數(shù)為2人,從成績(jī)?cè)?/span>![]() 和
和![]() 的學(xué)生中選兩人,將分?jǐn)?shù)段
的學(xué)生中選兩人,將分?jǐn)?shù)段![]() 的4人編號(hào)為
的4人編號(hào)為![]() ,
,![]() ,
,![]() ,
,![]() ,將
,將![]() 分?jǐn)?shù)段的2人編號(hào)為
分?jǐn)?shù)段的2人編號(hào)為![]() ,
,![]() ,從中任選兩人,則基本事件構(gòu)成集合
,從中任選兩人,則基本事件構(gòu)成集合![]() 共15個(gè),其中同一分?jǐn)?shù)段內(nèi)的事件所含基本事件為7個(gè),利用古典概型計(jì)算公式即可得出。
共15個(gè),其中同一分?jǐn)?shù)段內(nèi)的事件所含基本事件為7個(gè),利用古典概型計(jì)算公式即可得出。
(1)因?yàn)楦鹘M的頻率之和等于1,所以成績(jī)?cè)?/span>![]() 的頻率為
的頻率為![]() 。
。
補(bǔ)全頻率分布直方圖如圖所示:

(2)根據(jù)題意,60分及以上的分?jǐn)?shù)在![]() ,
,![]() ,
,![]() ,
,![]() 這四個(gè)組,其頻率之和為
這四個(gè)組,其頻率之和為![]() ,故本次考試的及格率為75%
,故本次考試的及格率為75%
利用中值估算學(xué)生成績(jī)的平均分,則有
![]()
所以本次考試的平均分為71分。
(3)成績(jī)?cè)?/span>![]() 的人數(shù)為
的人數(shù)為![]() 人,成績(jī)?cè)?/span>
人,成績(jī)?cè)?/span>![]() 的人數(shù)為
的人數(shù)為![]() 人
人
從成績(jī)?cè)?/span>![]() 和
和![]() 的學(xué)生中選兩人,將分?jǐn)?shù)段
的學(xué)生中選兩人,將分?jǐn)?shù)段![]() 的4人編號(hào)為
的4人編號(hào)為![]() ,
,![]() ,
,![]() ,
,![]() ,將
,將![]() 分?jǐn)?shù)段的2人編號(hào)為
分?jǐn)?shù)段的2人編號(hào)為![]() ,
,![]() ,從中任選兩人,則基本事件構(gòu)成集合
,從中任選兩人,則基本事件構(gòu)成集合
![]()
共15個(gè),其中同一分?jǐn)?shù)段內(nèi)所含基本事件為:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
共7個(gè),故概率![]()



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的定義域;
的定義域;
(2)若函數(shù)![]() 有且僅有一個(gè)零點(diǎn),求實(shí)數(shù)m的取值范圍;
有且僅有一個(gè)零點(diǎn),求實(shí)數(shù)m的取值范圍;
(3)任取![]() ,若不等式
,若不等式![]() 對(duì)任意
對(duì)任意![]() 恒成立,求實(shí)數(shù)m的取值范圍.
恒成立,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
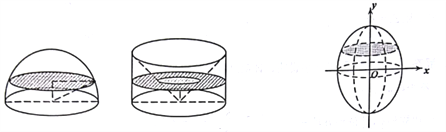
【題目】我國(guó)南北朝時(shí)間著名數(shù)學(xué)家祖暅提出了祖暅原理:“冪勢(shì)既同,則積不容異”.意思是:夾在兩平行平面間的兩個(gè)幾何體,被平行于這兩個(gè)平行平面的任何平面所載,若截得的兩個(gè)截面面積總相等,則這兩個(gè)幾何體的體積相等.為計(jì)算球的體積,構(gòu)造一個(gè)底面半徑和高都與球半徑相等的圓柱,然后再圓柱內(nèi)挖去一個(gè)以圓柱下底面圓心為頂點(diǎn),圓柱上底面為底面的圓錐,運(yùn)用祖暅原理可證明此幾何體與半球體積相等(任何一個(gè)平面所載的兩個(gè)截面面積都相等).將橢圓![]() 繞
繞![]() 軸旋轉(zhuǎn)一周后得一橄欖狀的幾何體,類(lèi)比上述方法,運(yùn)用祖暅原理可求得其體積等于( )
軸旋轉(zhuǎn)一周后得一橄欖狀的幾何體,類(lèi)比上述方法,運(yùn)用祖暅原理可求得其體積等于( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,已知三棱柱ABC-A1B1C1,側(cè)面ABB1A1為菱形,側(cè)面ACC1A1為正方形,側(cè)面ABB1A1⊥側(cè)面ACC1A1.
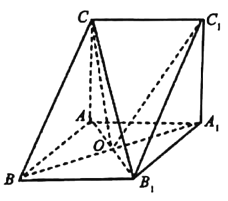
(1)求證:A1B⊥平面AB1C;
(2)若AB=2,∠ABB1=60°,求三棱錐C1-COB1的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() .
.
(1)當(dāng)![]() ,
,![]() 時(shí),求滿(mǎn)足
時(shí),求滿(mǎn)足![]() 的
的![]() 的值;
的值;
(2)若函數(shù)![]() 是定義在
是定義在![]() 上的奇函數(shù).
上的奇函數(shù).
①存在![]() ,使得不等式
,使得不等式![]() 有解,求實(shí)數(shù)
有解,求實(shí)數(shù)![]() 的取值范圍;
的取值范圍;
②若函數(shù)![]() 滿(mǎn)足
滿(mǎn)足![]() ,若對(duì)任意
,若對(duì)任意![]() 且
且![]() ,不等式
,不等式![]() 恒成立,求實(shí)數(shù)
恒成立,求實(shí)數(shù)![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】北京101中學(xué)校園內(nèi)有一個(gè)“少年湖”,湖的兩側(cè)有一個(gè)音樂(lè)教室和一個(gè)圖書(shū)館,如圖,若設(shè)音樂(lè)教室在A處,圖書(shū)館在B處,為測(cè)量A,B兩地之間的距離,某同學(xué)選定了與A,B不共線的C處,構(gòu)成△ABC,以下是測(cè)量的數(shù)據(jù)的不同方案:①測(cè)量∠A,AC,BC;②測(cè)量∠A,∠B,BC;③測(cè)量∠C,AC,BC;④測(cè)量∠A,∠C,∠B. 其中一定能唯一確定A,B兩地之間的距離的所有方案的序號(hào)是_______.

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】函數(shù)y=![]() 的圖象與函數(shù)y=2sinπx(﹣3≤x≤5)的圖象所有交點(diǎn)的橫坐標(biāo)之和等于( )
的圖象與函數(shù)y=2sinπx(﹣3≤x≤5)的圖象所有交點(diǎn)的橫坐標(biāo)之和等于( )
A.2 B.4 C.6 D.8
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】在直角坐標(biāo)系![]() 中, 橢圓
中, 橢圓![]() 的中心在坐標(biāo)原點(diǎn)
的中心在坐標(biāo)原點(diǎn)![]() ,其右焦點(diǎn)為
,其右焦點(diǎn)為![]() ,且點(diǎn)
,且點(diǎn)![]() 在橢圓
在橢圓![]() 上.
上.

(1)求橢圓![]() 的方程;
的方程;
(2)設(shè)橢圓的左、右頂點(diǎn)分別為![]() ,
,![]() 是橢圓上異于
是橢圓上異于![]() 的任意一點(diǎn),直線
的任意一點(diǎn),直線![]() 交橢圓
交橢圓![]() 于另一點(diǎn)
于另一點(diǎn)![]() ,直線
,直線![]() 交直線
交直線![]() 于
于![]() 點(diǎn), 求證:
點(diǎn), 求證:![]() 三點(diǎn)在同一條直線上
三點(diǎn)在同一條直線上
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
【題目】已知函數(shù)![]() ,對(duì)于任意的
,對(duì)于任意的![]()
![]() ,都有
,都有![]() , 當(dāng)
, 當(dāng)![]() 時(shí),
時(shí),![]() ,且
,且![]() .
.
( I ) 求![]() 的值;
的值;
(II) 當(dāng)![]() 時(shí),求函數(shù)
時(shí),求函數(shù)![]() 的最大值和最小值;
的最大值和最小值;
(III) 設(shè)函數(shù)![]() ,判斷函數(shù)g(x)最多有幾個(gè)零點(diǎn),并求出此時(shí)實(shí)數(shù)m的取值范圍.
,判斷函數(shù)g(x)最多有幾個(gè)零點(diǎn),并求出此時(shí)實(shí)數(shù)m的取值范圍.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com