【題目】中國古代名詞“芻童”原來是草堆的意思，古代用它作為長方體棱臺（上、下底面均為矩形額棱臺）的專用術語，關于“芻童”體積計算的描述，《九章算術》注曰：“倍上表，下表從之，亦倍小表，上表從之，各以其廣乘之，并，以高若深乘之，皆六面一.”其計算方法是：將上底面的長乘二，與下底面的長相加，再與上底面的寬相乘；將下底面的長乘二，與上底面的長相加，再與下底面的寬相乘；把這兩個數值相加，與高相乘，再取其六分之一，以此算法，現有上下底面為相似矩形的棱臺，相似比為
，高為3，且上底面的周長為6，則該棱臺的體積的最大值是（ ）
A. 14 B. 56 C. 
D. 63
雙基同步導航訓練系列答案
黃岡小狀元同步計算天天練系列答案科目：高中數學 來源： 題型：
【題目】上半年產品產量與單位成本資料如下：
月份 | 產量/千件 | 單位成本/元 |
1 | 2 | 73 |
2 | 3 | 72 |
3 | 4 | 71 |
4 | 3 | 73 |
5 | 4 | 69 |
6 | 5 | 68 |
且已知產量x與單位成本y具有線性相關關系.
(1)求出回歸方程.
(2)指出產量每增加1 000件時，單位成本平均變動多少?
(3)假定產量為6 000件時，單位成本為多少元?
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐
中，底面
為直角梯形， 
， 
，平面
平面
， 
為
的中點， 
是棱
上的點， 
， 
， 
．
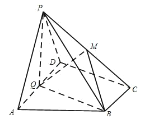
（1）求證：平面
平面
；
（2）若二面角
大小為
，求線段
的長．
查看答案和解析>>
科目：高中數學 來源： 題型：
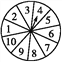
【題目】有一個轉盤游戲,轉盤被平均分成10等份(如圖所示),轉動轉盤,當轉盤停止后,指針指向的數字即為轉出的數字.游戲規(guī)則如下:兩個人參加,先確定猜數方案,甲轉動轉盤,乙猜,若猜出的結果與轉盤轉出的數字所表示的特征相符,則乙獲勝,否則甲獲勝.猜數方案從以下三種方案中選一種:
A.猜“是奇數”或“是偶數”
B.猜“是4的整數倍數”或“不是4的整數倍數”
C.猜“是大于4的數”或“不是大于4的數”
請回答下列問題:
(1)如果你是乙,為了盡可能獲勝,你將選擇哪種猜數方案,并且怎樣猜?為什么?
(2)為了保證游戲的公平性,你認為應制定哪種猜數方案?為什么?
(3)請你設計一種其他的猜數方案,并保證游戲的公平性.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】現從某班的一次期末考試中，隨機的抽取了七位同學的數學(滿分150分）、物理（滿分110分）成績如下表所示，數學、物理成績分別用特征量
表示，
特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
t | 101 | 124 | 119 | 106 | 122 | 118 | 115 |
y | 74 | 83 | 87 | 75 | 85 | 87 | 83 |
求
關于t的回歸方程；
（2）利用（1）中的回歸方程，分析數學成績的變化對物理成績的影響，并估計該班某學生數學成績130分時，他的物理成績(精確到個位).
附：回歸方程
中斜率和截距的最小二乘估計公式分別為：
． 
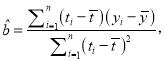
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】國際奧委會將于2017年9月15日在秘魯利馬召開130次會議決定2024年第33屆奧運會舉辦地。目前德國漢堡、美國波士頓等申辦城市因市民擔心賽事費用超支而相繼退出。某機構為調查我國公民對申辦奧運會的態(tài)度，選了某小區(qū)的100位居民調查結果統計如下:
（1）根據已有數據，把表格數據填寫完整；
（2）能否在犯錯誤的概率不超過5%的前提下認為不同年齡與支持申辦奧運無關？
（3）已知在被調查的年齡大于50歲的支持者中有5名女性，其中2位是女教師,現從這5名女性中隨機抽取3人，求至多有1位教師的概率.
附: 
， 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
：
的右焦點為
，且點
在橢圓上．
⑴求橢圓的標準方程；
⑵已知動直線
過點
且與橢圓交于
兩點．試問
軸上是否存在定點
,使得
恒成立？若存在，求出點Q的坐標；若不存在，請說明理由．
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
