Question

已知函數方程f（x）=x³+bx²+cx+d（b，c，d為常數），當k∈（-∞，0）∪（4，+∞）時，方程f（x）-k=0有且僅有一個實根，當k∈（0，4）時，方程f（x）-k=0有3個相異實根．給出下列4個命題：
①方程f（x）=4和f'（x）=0有且僅有一個相同的實根；
②方程f（x）=0和f'（x）=0有且僅有一個相同的實根；
③方程f（x）+3=0的任一實根都大于f（x）-1=0的任一實根；
④方程f（x）+5=0的任一實根都小于f（x）-2=0的任一實根．
其中正確命題的序號是    ．

Answer 1

【答案】分析：f（x）-k=0的根的問題可轉化為f（x）=k，即y=k和y=f（x）圖象交點個數問題．由題意y=f（x）圖象應為先增后減再增，極大值為4，極小值為0．
解答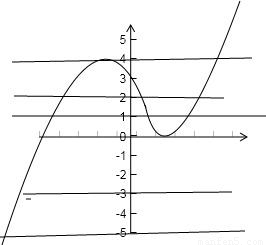：解：由題意y=f（x）圖象應為先增后減再增，
極大值為4，極小值為0．
f（x）-k=0的根的問題可轉化為f（x）=k，
即y=k和y=f（x）圖象交點個數問題．
故答案為：①②④
點評：本題考查方程根的問題，方程根的問題?函數的零點問題?兩個函數圖象的交點問題，轉化為數形結合求解．