
D
[解析] 依題意得0<a<1,于是由f(1-![]() )>1得loga(1-
)>1得loga(1-![]() )>logaa,0<1-
)>logaa,0<1-![]() <a,由此解得1<x<
<a,由此解得1<x<![]() ,因此不等式f(1-
,因此不等式f(1-![]() )>1的解集是(1,
)>1的解集是(1,![]() ),選D.
),選D.
科目:高中數學 來源: 題型:
D
[解析] ⊙C1:(x+a)2+y2=4的圓心C1(-a,0),半徑r1=2,⊙C2:x2+(y-b)2=1的圓心C2(0,b),半徑r2=1,
∵⊙C1與⊙C2外切,∴|C1C2|=r1+r2,
∴a2+b2=9,
∵(a+b)2=a2+b2+2ab≤2(a2+b2)=18,
∴a+b≤3![]() ,等號在a=b=
,等號在a=b=![]() 時成立.
時成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
過平行六面體ABCD-A1B1C1D1任意兩條棱的中點作直線,其中與平面DBB1D1平行的直線共有( )
A.4條 B.6條
C.8條 D.12條
[答案] D
[解析] 如圖所示,設M、N、P、Q為所在邊的中點,
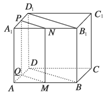
則過這四個點中的任意兩點的直線都與面DBB1D1平行,這種情形共有6條;同理,經過BC、CD、B1C1、C1D1四條棱的中點,也有6條;故共有12條,故選D.
查看答案和解析>>
科目:高中數學 來源: 題型:
解析:依題意得f(x)的圖象關于直線x=1對稱,f(x+1)=-f(x-1),f(x+2)=-f(x),f(x+4)=-f(x+2)=f(x),即函數f(x)是以4為周期的函數.由f(x)在[3,5]上是增函數與f(x)的圖象關于直線x=1對稱得,f(x)在[-3,-1]上是減函數.又函數f(x)是以4為周期的函數,因此f(x)在[1,3]上是減函數,f(x)在[1,3]上的最大值是f(1),最小值是f(3).
答案:A
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com