
(1)y=x2+![]() ;(2)y=|x+1|+|x-1|.
;(2)y=|x+1|+|x-1|.
思路分析:本題主要考查函數的最值及其求法.對于不同的函數采用不同的求法.(1)利用函數的單調性求最值;(2)可以畫圖像,也可以對解析式賦予幾何意義,數形結合求最值.
解:(1)(單調法)函數y=x2+![]() 的定義域是[0,+∞),可以證明函數y=x2+
的定義域是[0,+∞),可以證明函數y=x2+![]() 在定義域內是增函數,則有f(x)≥f(0)=0+0=0,即函數y=x2+x有最小值0,無最大值.
在定義域內是增函數,則有f(x)≥f(0)=0+0=0,即函數y=x2+x有最小值0,無最大值.
(2)解法一(圖像法):y=|x+1|+|x-1|=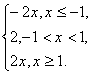 其圖像如圖所示.
其圖像如圖所示.
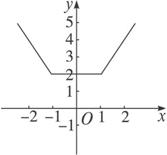
由圖像得函數的最小值是2,無最大值;
解法二(數形結合):函數的解析式y=|x+1|+|x-1|的幾何意義是:y是數軸上任意一點P到±1的對應點A,B的距離的和,即y=|PA|+|PB|,如圖所示,
![]()
觀察數軸可得|PA|+|PB|≥|AB|=2,即函數有最小值2,無最大值.


科目:高中數學 來源: 題型:
| 4 |
| x |
| 1 |
| x-2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 6 |
| x2 |
| 1 |
| 9 |
| x |
| 27 |
| 1 |
| b(a-b) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com