設P是橢圓
上的一點，F1、F2是焦點，若∠F1PF2=30°，則△PF1F2的面積為（ ）
A.
B.
C.
D.16
B
【解析】
試題分析：根據橢圓方程算出橢圓的焦點坐標為F1（﹣3，0）、F2（3，0）．由橢圓的定義|PF1|+|PF2|=10，△PF1F2中用余弦定理得到|PF1|2+|PF2|2﹣2|PF1|•|PF2|cos30°=36，兩式聯解可得|PF1|•|PF2|=64（2﹣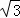
），最后根據三角形面積公式即可算出△PF1F2的面積．
【解析】
∵橢圓方程為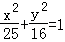
，
∴a2=25，b2=16，得a=5且b=4，c=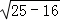
=3，
因此，橢圓的焦點坐標為F1（﹣3，0）、F2（3，0）．
根據橢圓的定義，得|PF1|+|PF2|=2a=10
∵△PF1F2中，∠F1PF2=30°，
∴|F1F2|2=|PF1|2+|PF2|2﹣2|PF1|•|PF2|cos30°=4c2=36，
可得（|PF1|+|PF2|）2=36+（2+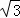）|PF1|•|PF2|=100
因此，|PF1|•|PF2|=
=64（2﹣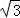
），
可得△PF1F2的面積為S=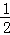
•|PF1|•|PF2|sin30°=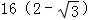
故選：B
七彩題卡口算應用一點通系列答案科目：高中數學 來源：[同步]2014年蘇教版選修1-2 3.2復數的四則運算練習卷（解析版） 題型：選擇題
如果復數（m2+i）（1+mi）是實數，則實數m=（ ）
A.1 B.﹣1 C.
D.
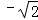
查看答案和解析>>
科目：高中數學 來源：[同步]2014年蘇教版選修1-1 3.2導數的運算練習卷（解析版） 題型：填空題
設μ∈R，函數f（x）=ex+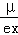
的導函數是f′（x），且f′（x）是奇函數，若曲線y=f（x）的一條切線的斜率是
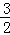，則該切點的橫坐標是 ．
查看答案和解析>>
科目：高中數學 來源：[同步]2014年蘇教版選修1-1 2.5圓錐曲線與方程練習卷（解析版） 題型：解答題
直線l：y=mx+1，雙曲線C：3x2﹣y2=1，問是否存在m的值，使l與C相交于A，B兩點，且以AB為直徑的圓過原點．
查看答案和解析>>
科目：高中數學 來源：[同步]2014年蘇教版選修1-1 2.5圓錐曲線與方程練習卷（解析版） 題型：選擇題
命題甲：“雙曲線C的方程為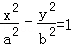
”，命題乙：“雙曲線C的漸近線方程為
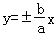”，那么甲是乙的（ ）
A.充分不必要條件 B.必要不充分條件
C.充要條件 D.既不充分也不必要條件
查看答案和解析>>
科目：高中數學 來源：[同步]2014年蘇教版選修1-1 2.4拋物線練習卷（解析版） 題型：解答題
拋物線的頂點是橢圓16x2+25y2=400的中心，而焦點是橢圓的右焦點，求此拋物線的方程．
查看答案和解析>>
科目：高中數學 來源：[同步]2014年蘇教版選修1-1 2.1圓錐曲線練習卷（解析版） 題型：選擇題
F1，F2是橢圓
的兩個焦點，A為橢圓上一點，且∠AF1F2=45°，則三角形AF1F2的面積為（ ）
A.7 B.
C.
D.
查看答案和解析>>
科目：高中數學 來源：[同步]2014年蘇教版必修四 1.1任意角、弧度制練習卷（解析版） 題型：填空題
若角β的終邊與60°角的終邊相同，在[0°，360°）內，終邊與角
的終邊相同的角為 ．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
=1的右頂點為焦點的拋物線的標準方程為 ．