
(本小題滿分13分)
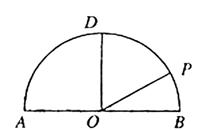
如圖,在以點(diǎn)O為圓心,|AB|=4為直徑的半圓ADB中,OD⊥AB,P是半圓弧上一點(diǎn),
∠POB=30°,曲線C是滿足||MA|-|MB||為定值的動(dòng)點(diǎn)M的軌跡,且曲線C過(guò)點(diǎn)P。
(Ⅰ)建立適當(dāng)?shù)钠矫嬷苯亲鴺?biāo)系,求曲線C的方程;
(Ⅱ)設(shè)過(guò)點(diǎn)D的直線l與曲線C相交于不同的兩點(diǎn)E、F。若△OEF的面積不小于2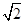 ,求直線l斜率的取值范圍。
,求直線l斜率的取值范圍。
(Ⅰ)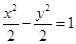
(Ⅱ)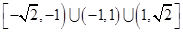
【解析】
(Ⅰ)解法1:以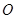 為原點(diǎn),
為原點(diǎn),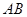 、
、 所在直線分別為
所在直線分別為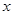 軸、
軸、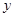 軸,建立平面直角坐標(biāo)系,則
軸,建立平面直角坐標(biāo)系,則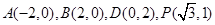 ,
,
由題意得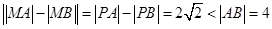 。
。
所以曲線 是以原點(diǎn)為中心,
是以原點(diǎn)為中心, 、
、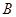 為焦點(diǎn)的雙曲線。
為焦點(diǎn)的雙曲線。
設(shè)實(shí)半軸長(zhǎng)為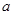 ,虛半軸長(zhǎng)為
,虛半軸長(zhǎng)為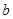 ,半焦距為
,半焦距為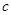 ,
,
則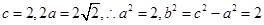
所以曲線 的方程為
的方程為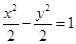 。
。
解法2:同解法1建立平面直角坐標(biāo)系,則由題意可得
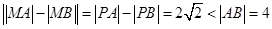
所以曲線 是以原點(diǎn)為中心,
是以原點(diǎn)為中心, 、
、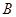 為焦點(diǎn)的雙曲線。
為焦點(diǎn)的雙曲線。
設(shè)雙曲線的方程為
則由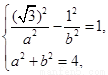 解得
解得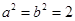 ,
,
所以曲線 的方程為
的方程為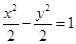 。
。
(Ⅱ)解法1:由題意,可設(shè)直線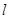 的方程為
的方程為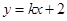 ,代入雙曲線
,代入雙曲線 的方程并整理得
的方程并整理得
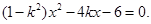 ……①
……①
因?yàn)榕c雙曲線相交不同的兩點(diǎn)E、F,

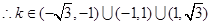 ……②
……②
設(shè)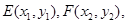 則由①式得
則由①式得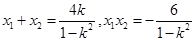 ,于是
,于是
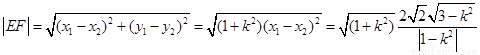 .
.
而原點(diǎn)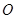 到直線
到直線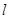 的距離
的距離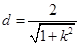 ,
,
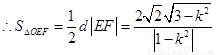
若 面積不小于
面積不小于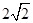 ,即
,即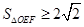 ,則有
,則有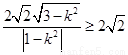 ,
,
解得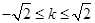 ……③
……③
綜合②、③知,直線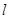 的斜率的取值范圍為
的斜率的取值范圍為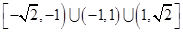 。
。
解法2:依題意,可設(shè)直線l的方程為y=kx+2,代入雙曲線C的方程并整理,
得(1-k2)x2-4kx-6=0。

∵直線l與雙曲線C相交于不同的兩點(diǎn)E、F,
∴

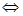
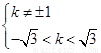 。
。
∴k∈(-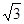 ,-1)∪(-1,1)∪(1,
,-1)∪(-1,1)∪(1,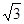 )。
)。
設(shè)E(x1,y1),F(x2,y2),則由①式得
|x1-x2|=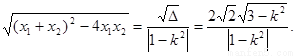 ③
③
當(dāng)E、F在同一支上時(shí)(如左圖所示),
S△OEF=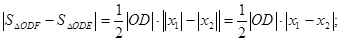
當(dāng)E、F在不同支上時(shí)(如右圖所示)。
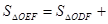 S△ODE=
S△ODE=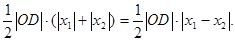
綜上得S△OEF=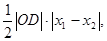 于是
于是
由|OD|=2及③式,得S△OEF=
若△OEF面積不小于2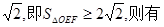
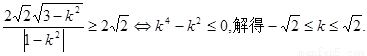 ④
④
綜合②、④知,直線l的斜率的取值范圍為[-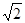 ,-1]∪(-1,1)∪(1,
,-1]∪(-1,1)∪(1,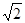 )。
)。
本題條件涉及到一動(dòng)點(diǎn)到兩定點(diǎn)距離差的絕對(duì)值,容易想到雙曲線的定義,所以第(1)問(wèn)只要求求了出雙曲線方程中的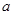 與
與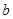 。第(2)涉及到直線與圓錐曲線相交的問(wèn)題,一般是要設(shè)出直線聯(lián)立曲線,再用韋達(dá)定理,本問(wèn)要解法的是求范圍的問(wèn)題,其不等式在第(2)問(wèn)中已給出,所以只需寫出三角形面積的表達(dá)式。
。第(2)涉及到直線與圓錐曲線相交的問(wèn)題,一般是要設(shè)出直線聯(lián)立曲線,再用韋達(dá)定理,本問(wèn)要解法的是求范圍的問(wèn)題,其不等式在第(2)問(wèn)中已給出,所以只需寫出三角形面積的表達(dá)式。


 教材全解字詞句篇系列答案
教材全解字詞句篇系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源:2015屆江西省高一第二次月考數(shù)學(xué)試卷(解析版) 題型:解答題
(本小題滿分13分)已知函數(shù)
 .
.
(1)求函數(shù) 的最小正周期和最大值;
的最小正周期和最大值;
(2)在給出的直角坐標(biāo)系中,畫出函數(shù) 在區(qū)間
在區(qū)間 上的圖象.
上的圖象.
(3)設(shè)0<x< ,且方程
,且方程 有兩個(gè)不同的實(shí)數(shù)根,求實(shí)數(shù)m的取值范圍.
有兩個(gè)不同的實(shí)數(shù)根,求實(shí)數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年福建省高三年級(jí)八月份月考試卷理科數(shù)學(xué) 題型:解答題
(本小題滿分13分)已知定義域?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012052519321600001521/SYS201205251933396875338731_ST.files/image001.png">的函數(shù) 是奇函數(shù).
是奇函數(shù).
(1)求 的值;(2)判斷函數(shù)
的值;(2)判斷函數(shù) 的單調(diào)性;
的單調(diào)性;
(3)若對(duì)任意的 ,不等式恒成立
,不等式恒成立 ,求k的取值范圍.
,求k的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2011-2012學(xué)年福建省高三年級(jí)八月份月考試卷理科數(shù)學(xué) 題型:解答題
(本小題滿分13分)已知集合 ,
,  ,
, .
.
(1)求 (∁
(∁ ; (2)若
; (2)若 ,求
,求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:河南省09-10學(xué)年高二下學(xué)期期末數(shù)學(xué)試題(理科) 題型:解答題
(本小題滿分13分)如圖,正三棱柱 的所有棱長(zhǎng)都為2,
的所有棱長(zhǎng)都為2, 為
為 的中點(diǎn)。
的中點(diǎn)。
(Ⅰ)求證: ∥平面
∥平面 ;
;
(Ⅱ)求異面直線 與
與 所成的角。www.7caiedu.cn
所成的角。www.7caiedu.cn

[來(lái)源:KS5
U.COM
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:2010-2011學(xué)年福建省高三5月月考調(diào)理科數(shù)學(xué) 題型:解答題
(本小題滿分13分)
已知 為銳角,且
為銳角,且 ,函數(shù)
,函數(shù) ,數(shù)列{
,數(shù)列{ }的首項(xiàng)
}的首項(xiàng) .
.
(1) 求函數(shù) 的表達(dá)式;
的表達(dá)式;
(2)在 中,若
中,若 A=2
A=2 ,
, ,BC=2,求
,BC=2,求 的面積
的面積
(3) 求數(shù)列 的前
的前 項(xiàng)和
項(xiàng)和
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com