
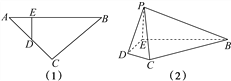
【題目】如圖(1),等腰直角三角形ABC的底邊AB=4,點D在線段AC上,DE⊥AB于E,現將△ADE沿DE折起到△PDE的位置(如圖(2)).
(1)求證:PB⊥DE;
(2)若PE⊥BE,PE=1,求點B到平面PEC的距離.
【答案】(1)詳見解析(2)![]()
【解析】試題分析:(1)根據線面垂直的判定定理和性質定理進行證明,(2)由(1)知PE⊥平面BEDC,在△EDC中,由余弦定理得EC=![]() ,S△PEC=
,S△PEC=![]() ×PE×EC=
×PE×EC=![]() .利用等體積法VP-BEC=VB-PEC進行求解即可得點B到平面PEC的距離.
.利用等體積法VP-BEC=VB-PEC進行求解即可得點B到平面PEC的距離.
試題解析:
(1)∵DE⊥AB,∴DE⊥PE,DE⊥EB.
又∵PE∩BE=E,∴DE⊥平面PEB.∵PB平面PEB,∴PB⊥DE.
(2)由(1)知DE⊥PE,且PE⊥BE,DE∩BE=E,∴PE⊥平面BEDC.
連接EC,∵PE=1,
∴DE=PE=1,AD=DC=![]() .
.
在△EDC中,∠EDC=135°,由余弦定理得
EC2=DE2+DC2-2DE×DC×cos∠EDC=1+2-2![]() ×(-
×(-![]() )=5,
)=5,
∴EC=![]() ,∴S△PEC=
,∴S△PEC=![]() ×PE×EC=
×PE×EC=![]() .
.
設點B到平面PEC的距離為h,則由VP-BEC=VB-PEC得![]() S△PEC·h=
S△PEC·h=![]() S△BEC·PE,
S△BEC·PE,
∴![]() h=
h=![]() ×3×2×1,∴h=
×3×2×1,∴h=![]() .
.


科目:高中數學 來源: 題型:
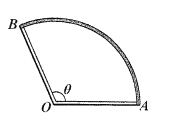
【題目】園林管理處擬在公園某區域規劃建設一半徑為![]() 米,圓心角為
米,圓心角為![]() (弧度)的扇形觀景水池,其中
(弧度)的扇形觀景水池,其中![]() ,
, ![]() 為扇形
為扇形![]() 的圓心,同時緊貼水池周邊(即:
的圓心,同時緊貼水池周邊(即: ![]() 和
和![]() 所對的圓弧)建設一圈理想的無寬度步道.要求總預算費用不超過24萬元,水池造價為每平方米400元,步道造價為每米1000元.
所對的圓弧)建設一圈理想的無寬度步道.要求總預算費用不超過24萬元,水池造價為每平方米400元,步道造價為每米1000元.
(1)若總費用恰好為24萬元,則當![]() 和
和![]() 分別為多少時,可使得水池面積最大,并求出最大面積;
分別為多少時,可使得水池面積最大,并求出最大面積;
(2)若要求步道長為105米,則可設計出的水池最大面積是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的方程為
的方程為![]() (
(![]() ,
, ![]() 為常數).
為常數).
(1)判斷曲線![]() 的形狀;
的形狀;
(2)設曲線![]() 分別與
分別與![]() 軸,
軸, ![]() 軸交于點
軸交于點![]() ,
, ![]() (
(![]() ,
, ![]() 不同于原點
不同于原點![]() ),試判斷
),試判斷![]() 的面積
的面積![]() 是否為定值?并證明你的判斷;
是否為定值?并證明你的判斷;
(3)設直線![]() :
: ![]() 與曲線
與曲線![]() 交于不同的兩點
交于不同的兩點![]() ,
, ![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】祖暅原理也就是“等積原理”,它是由我國南北朝杰出的數學家祖沖之的兒子祖暅首先提出來的,祖暅原理的內容是:夾在兩個平行平面間的兩個幾何體,被平行于這兩個平行平面的平面所截,如果截得兩個截面的面積總相等,那么這兩個幾何體的體積相等.已知,兩個平行平面間有三個幾何體,分別是三棱錐、四棱錐、圓錐(高度都為![]() ),其中:三棱錐的底面是正三角形(邊長為
),其中:三棱錐的底面是正三角形(邊長為![]() ),四棱錐的底面是有一個角為
),四棱錐的底面是有一個角為![]() 的菱形(邊長為
的菱形(邊長為![]() ),圓錐的體積為
),圓錐的體積為![]() ,現用平行于這兩個平行平面的平面去截三個幾何體,如果截得的三個截面的面積相等,那么,下列關系式正確的是( )
,現用平行于這兩個平行平面的平面去截三個幾何體,如果截得的三個截面的面積相等,那么,下列關系式正確的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=-f′(0)ex+2x,點P為曲線y=f(x)在點(0,f(0))處的切線l上的一點,點Q在曲線y=ex上,則|PQ|的最小值為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(2-a)lnx+![]() +2ax.
+2ax.
(1)當a<0時,討論f(x)的單調性;
(2)若對任意的a∈(-3,-2),x1,x2∈[1,3],恒有(m+ln 3)a-2ln 3>|f(x1)-f(x2)|成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解學生的身體狀況,某校隨機抽取了一批學生測量體重,經統計,這批學生的體重數據(單位:千克)全部介于![]() 至
至![]() 之間,將數據分成以下
之間,將數據分成以下![]() 組,第一組
組,第一組![]() ,第二組
,第二組![]() ,第三組
,第三組![]() ,第四組,第五組
,第四組,第五組![]() ,得到如圖所示的頻率分布直方圖,現采用分層抽樣的方法,從第
,得到如圖所示的頻率分布直方圖,現采用分層抽樣的方法,從第![]() 、
、![]() 、
、![]() 組中隨機抽取
組中隨機抽取![]() 名學生做初檢.
名學生做初檢.
(Ⅰ)求每組抽取的學生人數.
(Ⅱ)若從![]() 名學生中再次隨機抽取
名學生中再次隨機抽取![]() 名學生進行復檢,求這
名學生進行復檢,求這![]() 名學生不在同一組的概率.
名學生不在同一組的概率.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某互聯網理財平臺為增加平臺活躍度決定舉行邀請好友拿獎勵活動,規則是每邀請一位好友在該平臺注冊,并購買至少1萬元的12月定期,邀請人可獲得現金及紅包獎勵,現金獎勵為被邀請人理財金額的![]() ,且每邀請一位最高現金獎勵為300元,紅包獎勵為每邀請一位獎勵50元.假設甲邀請到乙、丙兩人,且乙、丙兩人同意在該平臺注冊,并進行理財,乙、丙兩人分別購買1萬元、2萬元、3萬元的12月定期的概率如下表:
,且每邀請一位最高現金獎勵為300元,紅包獎勵為每邀請一位獎勵50元.假設甲邀請到乙、丙兩人,且乙、丙兩人同意在該平臺注冊,并進行理財,乙、丙兩人分別購買1萬元、2萬元、3萬元的12月定期的概率如下表:
理財金額 |
|
|
|
乙理財相應金額的概率 |
|
|
|
丙理財相應金額的概率 |
|
|
|
(1)求乙、丙理財金額之和不少于5萬元的概率;
(2)若甲獲得獎勵為![]() 元,求
元,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com