
 (
( ).
). 時,求函數
時,求函數 的極值;
的極值;  ,不等式
,不等式 恒成立,求實數
恒成立,求實數 的取值范圍.
的取值范圍.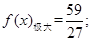
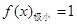 ;(Ⅱ)
;(Ⅱ)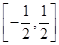 .
.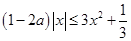 恒成立,然后分類討論思想,即對
恒成立,然后分類討論思想,即對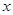 的正負討論和分離參數法,得到不同的不等式,進而利用均值不等式探求
的正負討論和分離參數法,得到不同的不等式,進而利用均值不等式探求 的取值范圍.
的取值范圍. 時,
時,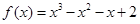 ,
,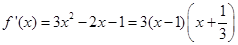 , 2分
, 2分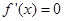 ,解得
,解得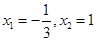 .
. 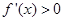 時,得
時,得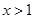 或
或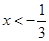 ;當
;當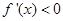 時,得
時,得 . 4分
. 4分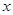 變化時,
變化時,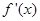 ,
, 的變化情況如下表:
的變化情況如下表: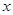 | 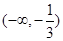 | 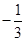 | 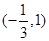 | 1 | 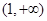 |
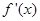 | + | 0 | 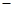 | 0 | + |
 | 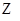 | 極大 | 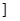 | 極小 | 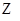 |
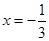 時,函數
時,函數 有極大值,
有極大值,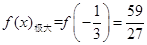 ; 5分
; 5分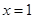 時,函數
時,函數 有極大值,
有極大值,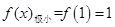 , 6分
, 6分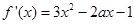 ,∴對
,∴對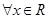 ,
, 恒成立,即
恒成立,即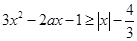
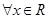 恒成立, 7分
恒成立, 7分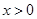 時,有
時,有 ,即
,即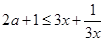 對
對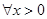 恒成立, 9分
恒成立, 9分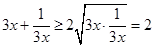 ,當且僅當
,當且僅當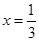 時等號成立,
時等號成立,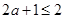 ,解得
,解得 11分
11分 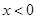 時,有
時,有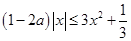 ,即
,即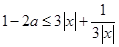 對
對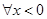 恒成立, 12分
恒成立, 12分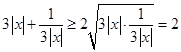 ,當且僅當
,當且僅當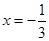 時等號成立,
時等號成立,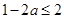 ,解得
,解得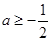 13分
13分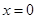 時,
時, .
. 的取值范圍為
的取值范圍為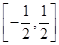 . 14分
. 14分

 點睛新教材全能解讀系列答案
點睛新教材全能解讀系列答案 小學教材完全解讀系列答案
小學教材完全解讀系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com