Question

【題目】給出下列命題：

①若 ， 是第一象限角且 ，則 ；

②函數 在上是減函數；

③ 是函數 的一條對稱軸；

④函數 的圖象關于點 成中心對稱；

⑤設 ，則函數 的最小值是，其中正確命題的序號為 __________．

Answer 1

【答案】③⑤

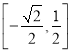【解析】對于①，時， ，而，故①錯誤；對于②，在上遞增，故②錯誤；對于③，時， ， 是的對稱軸，故③正確；對于④，時， 不是的對稱中心，故④錯誤；對于⑤，，設因為 ，所以,則 ， 在上遞增，在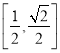 上遞減，因為 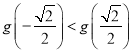可得時， ，即函數 的最小值是，故⑤正確，故答案為③⑤.

【 方法點睛】本題主要通過對多個命題真假的判斷，綜合考查三角函數的單調性、三角函數的奇偶性、三角函數的圖象與性質，屬于難題.這種題型綜合性較強，也是高考的命題熱點，同學們往往因為某一處知識點掌握不好而導致“全盤皆輸”，因此做這類題目更要細心、多讀題，盡量挖掘出題目中的隱含條件，另外，要注意從簡單的自己已經掌握的知識點入手，然后集中精力突破較難的命題.