
【題目】設函數![]() ,
,![]() .
.
(1)求函數![]() 的單調區間;
的單調區間;
(2)討論函數![]() 的零點個數
的零點個數
【答案】(1)當![]() 時,函數
時,函數![]() 的增區間是
的增區間是![]() 和
和![]() ,減區間是
,減區間是![]() ;
;
當![]() 時,函數
時,函數![]() 的增區間是
的增區間是![]() ,無減區間;
,無減區間;
當![]() 時,函數
時,函數![]() 的增區間是
的增區間是![]() 和
和![]() ,減區間是
,減區間是![]() .
.
(2)當![]() 時,函數
時,函數![]() 存在唯一零點.
存在唯一零點.
【解析】
(1)根據利用導數求函數單調區間的步驟,先求出函數的導數,然后在定義域內解含參的不等式,分類討論即可求出;
(2)由(1)可知函數的單調性,再結合零點存在性定理即可判斷出函數的零點個數.
(1)函數![]() 的定義域為
的定義域為![]() ,
,![]()
當![]() 時,由
時,由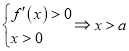 或
或![]() ,由
,由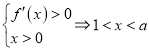 ;
;
當![]() 時,
時,![]() ;
;
當![]() 時,由
時,由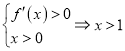 或
或![]() ,
,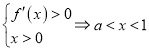
綜上,當![]() 時,函數
時,函數![]() 的增區間是
的增區間是![]() 和
和![]() ,減區間是
,減區間是![]() ;
;
當![]() 時,函數
時,函數![]() 的增區間是
的增區間是![]() ,無減區間;
,無減區間;
當![]() 時,函數
時,函數![]() 的增區間是
的增區間是![]() 和
和![]() ,減區間是
,減區間是![]() .
.
(2)由(1)可知,
①當![]() 時,函數
時,函數![]() 在
在![]() 和
和![]() 上遞增,在
上遞增,在![]() 上遞減,
上遞減,
所以,![]() ,
,![]() ,但是,
,但是,
當![]() 時,
時,![]() ,存在
,存在![]() ,故
,故![]() ,即在
,即在![]() 上存在唯一零點;
上存在唯一零點;
②當![]() 時,函數
時,函數![]() 在
在![]() 遞增,
遞增,![]() ,
,![]() ,
,
即在![]() 上存在唯一零點;
上存在唯一零點;
③當![]() 時,函數
時,函數![]() 在
在![]() 和
和![]() 上遞增,在
上遞增,在![]() 上遞減,
上遞減,
所以,![]() ,
,![]() ,但是,
,但是,
當![]() 時,
時,![]() ,存在
,存在![]() ,故
,故![]() ,即在
,即在![]() 上存在唯一零點.
上存在唯一零點.
綜上,當![]() 時,函數
時,函數![]() 存在唯一零點.
存在唯一零點.


科目:高中數學 來源: 題型:
【題目】一個口袋內有3個不同的紅球,4個不同的白球
(1)從中任取3個球,紅球的個數不比白球少的取法有多少種?
(2)若取一個紅球記2分,取一個白球記1分,從中任取4個球,使總分不少于6分的取法有多少種?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,圓盤上有一指針,開始時指向圓盤的正上方.指針每次順時針方向繞圓盤中心轉動一角![]() ,且
,且![]() ,經2004次旋轉,第一次回到了其初始位置,即又指向了圓盤的正上方.試問:
,經2004次旋轉,第一次回到了其初始位置,即又指向了圓盤的正上方.試問:![]() 有多少個可能的不同值?
有多少個可能的不同值?

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直線l的極坐標方程為θ=α(ρ∈R,ρ≠0),其中α∈[0,π),曲線C1的參數方程為![]() (t為參數),圓C2的普通方程為x2+y2+2
(t為參數),圓C2的普通方程為x2+y2+2![]() x=0.
x=0.
(1)求C1,C2的極坐標方程;
(2)若l與C1交于點A,l與C2交于點B,當|AB|=2時,求△ABC2的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著智能手機的普及,各類手機娛樂軟件也如雨后春筍般涌現. 如表中統計的是某手機娛樂軟件自2018年8月初推出后至2019年4月底的月新注冊用戶數,記月份代碼為![]() (如
(如![]() 對應于2018年8月份,
對應于2018年8月份,![]() 對應于2018年9月份,…,
對應于2018年9月份,…,![]() 對應于2019年4月份),月新注冊用戶數為
對應于2019年4月份),月新注冊用戶數為![]() (單位:百萬人)
(單位:百萬人)
![]()
(1)請依據上表的統計數據,判斷月新注冊用戶與月份線性相關性的強弱;
(2)求出月新注冊用戶關于月份的線性回歸方程,并預測2019年5月份的新注冊用戶總數.
參考數據:![]() ,
,![]() ,
,![]() .
.
回歸直線的斜率和截距公式: ,
,![]() .
.
相關系數 (當
(當![]() 時,認為兩相關變量相關性很強. )
時,認為兩相關變量相關性很強. )
注意:兩問的計算結果均保留兩位小數
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 、
、![]() 是兩條不同的直線,
是兩條不同的直線,![]() 、
、![]() 、
、![]() 是三個不同的平面,則
是三個不同的平面,則![]() 的一個充分條件是( )
的一個充分條件是( )
A.存在一條直線![]() ,
,![]() ,
,![]()
B.存在一條直線![]() ,
,![]() ,
,![]()
C.存在一個平面![]() ,滿足
,滿足![]() ,
,![]()
D.存在兩條異面直線![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com