
如圖,![]() 兩點(diǎn)分別在射線OS、OT上移動(dòng),且
兩點(diǎn)分別在射線OS、OT上移動(dòng),且![]() O為坐標(biāo)原點(diǎn),動(dòng)點(diǎn)P滿足
O為坐標(biāo)原點(diǎn),動(dòng)點(diǎn)P滿足![]()
(Ⅰ)求m?n的值;
(Ⅱ)求點(diǎn)P的軌跡C的方程,并說(shuō)明它表示怎么樣的曲線;
(Ⅲ)若直線l過(guò)點(diǎn)E(2,0)交(Ⅱ)中曲線C于M、N兩點(diǎn)(M、N、E三點(diǎn)互不相同),且![]() 求l的方程.
求l的方程.

解:(Ⅰ)由已知得![]()
![]()
![]()
(Ⅱ)設(shè)P點(diǎn)坐標(biāo)為(x,y)(x>0),由![]() 得
得
![]()
![]()
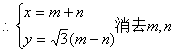 可得
可得
![]()
∴P點(diǎn)的軌跡方程為![]()
它表示以坐標(biāo)原點(diǎn)為中心,焦點(diǎn)在x軸上,且實(shí)軸長(zhǎng)為2,焦距為4的雙曲線
![]() 的右支
的右支
(Ⅲ)設(shè)直線l的方程為![]() ,將其代入C的方程得
,將其代入C的方程得
![]()
即![]()
易知![]() (否則,直線l的斜率為
(否則,直線l的斜率為![]() ,它與漸近線平行,不符合題意)
,它與漸近線平行,不符合題意)
又△144t2-36![]()
設(shè)![]()
∵l與C的兩個(gè)交點(diǎn)M,N在y軸右側(cè)
![]()
![]()
![]()
![]()
![]() ,
,
又∵t=0不合題意
![]()
又由![]() 同理可得
同理可得
![]()
由![]()
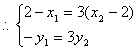
由![]()
由![]()
消去![]()
解之得:![]() ,滿足
,滿足![]()
故所求直線l存在,其方程為:![]()



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:
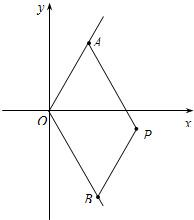 如圖,A(m,
如圖,A(m,| 3 |
| 3 |
| OA |
| OB |
| 1 |
| 2 |
| OP |
| OA |
| OB |
| ME |
| EN |
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源:天利38套《2008全國(guó)各省市高考模擬試題匯編(大綱版)》、數(shù)學(xué)理 題型:044
如圖,![]() 兩點(diǎn)分別在射線OS、OT上移動(dòng),且
兩點(diǎn)分別在射線OS、OT上移動(dòng),且![]() ·
·![]() =-
=-![]() ,O為坐標(biāo)原點(diǎn),動(dòng)點(diǎn)P滿足
,O為坐標(biāo)原點(diǎn),動(dòng)點(diǎn)P滿足![]() =
=![]() +
+![]() .
.

(Ⅰ)求m·n的值;
(Ⅱ)求點(diǎn)P的軌跡C的方程,并說(shuō)明它表示怎樣的曲線;
(Ⅲ)若直線l過(guò)點(diǎn)E(2,0)交(Ⅱ)中曲線C于M、N兩點(diǎn)(M、N、E三點(diǎn)互不相同),且![]() =3
=3![]() ,求l的方程.
,求l的方程.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
(08年聊城市二模) (12分) 如圖,![]() 兩點(diǎn)分別在射線OS、OT上移動(dòng),
兩點(diǎn)分別在射線OS、OT上移動(dòng),
且![]() ,O為坐標(biāo)原點(diǎn),動(dòng)點(diǎn)P滿足
,O為坐標(biāo)原點(diǎn),動(dòng)點(diǎn)P滿足![]()
(I)求![]() 的值;
的值;
(II)求點(diǎn)P的軌跡C的方程,并說(shuō)明它表示怎樣的曲線?
(III)若直線l過(guò)點(diǎn)E(2,0)交(II)中曲線C于M、N兩點(diǎn),且![]() 的方程。
的方程。

查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:
如圖, ![]() 兩點(diǎn)分別在射線OS,OT上移動(dòng),
兩點(diǎn)分別在射線OS,OT上移動(dòng),
且![]() ,O為坐標(biāo)原點(diǎn),動(dòng)點(diǎn)P滿足
,O為坐標(biāo)原點(diǎn),動(dòng)點(diǎn)P滿足![]() .
.
(1)求![]() 的值
的值
(2)求點(diǎn)P的軌跡C的方程,并說(shuō)明它表示怎樣的曲線.
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com