
【題目】如圖,CA,CB分別與圓O切于A,B兩點,AE是直徑,OF平分∠BOE交CB的延長線于F,BD∥AC. 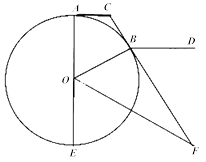
(1)證明:OB2=BCBF;
(2)證明:∠DBF=∠AOB.
【答案】
(1)證明:連接OC,由CA,CB為切線,可得CA=CB,
OA=OB,OC=OC,
即有△OAC≌△OBC,
即有∠AOC=∠BOC,
又OF平分∠BOE交CB的延長線于F,
可得∠EOF=∠BOF,
則∠FOC=∠FOB+∠BOC=∠EOF+∠AOC=90°,
在直角三角形COF中,OB為斜邊CF上的高,
由射影定理,可得OB2=BCBF

(2)證明:由∠CAO=∠CBO=90°,可得
四點C,A,O,B共圓,延長AC至M,
即有∠MCB=∠AOB,
由BD∥AC,可得∠DBF=∠MCB,
即有∠DBF=∠AOB
【解析】(1)連接OC,運用切線的性質,可得△OAC≌△OBC,結合內角平分線的定義,可得∠FOC=90°,由直角三角形的射影定理,即可得證;(2)由對角互補,可得四點C,A,O,B共圓,延長AC至M,運用兩直線平行的性質,即可得證.


 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:高中數學 來源: 題型:
【題目】甲乙兩人各有相同的小球10個,在每人的10個小球中都有5個標有數字1,3個標有數字2,2個標有數字3。兩人同時分別從自己的小球中任意抽取1個,規定:若抽取的兩個小球上的數字相同,則甲獲勝,否則乙獲勝,求乙獲勝的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數fn(x)=﹣xn+3ax(a∈R,n∈N+),若對任意的x1 , x2∈[﹣1,1],都有|f3(x1)﹣f3(x2)|≤1,則a的取值范圍是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]
]
D.[ ![]() ,
, ![]() ]
]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知雙曲線方程為![]() ,問:是否存在過點M(1,1)的直線l,使得直線與雙曲線交于P,Q兩點,且M是線段PQ的中點?如果存在,求出直線的方程,如果不存在,請說明理由.
,問:是否存在過點M(1,1)的直線l,使得直線與雙曲線交于P,Q兩點,且M是線段PQ的中點?如果存在,求出直線的方程,如果不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= ![]() (a>0,且a≠1)在R上單調遞減,且關于x的方程|f(x)|=2﹣x恰好有兩個不相等的實數解,則a的取值范圍是( )
(a>0,且a≠1)在R上單調遞減,且關于x的方程|f(x)|=2﹣x恰好有兩個不相等的實數解,則a的取值范圍是( )
A.(0, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[ ![]() ,
, ![]() ]∪{
]∪{ ![]() }
}
D.[ ![]() ,
, ![]() )∪{
)∪{ ![]() }
}
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法錯誤的是_____________.
①.如果命題“![]() ”與命題“
”與命題“![]() 或
或![]() ”都是真命題,那么命題
”都是真命題,那么命題![]() 一定是真命題.
一定是真命題.
②.命題![]() ,則
,則![]()
③.命題“若![]() ,則
,則![]() ”的否命題是:“若
”的否命題是:“若![]() ,則
,則![]() ”
”
④.特稱命題 “![]() ,使
,使![]() ”是真命題.
”是真命題.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com