
【題目】已知冪函數f(x)=(3m2﹣2m)x![]() 在(0,+∞)上單調遞增,g(x)=x2﹣4x+t.
在(0,+∞)上單調遞增,g(x)=x2﹣4x+t.
(1)求實數m的值;
(2)當x∈[1,9]時,記f(x),g(x)的值域分別為集合A,B,設命題p:x∈A,命題q:x∈B,若命題q是命題p的必要不充分條件,求實數t的取值范圍.
科目:高中數學 來源: 題型:
【題目】某校從參加某次知識競賽的同學中,選取60名同學將其成績(單位:分.百分制,均為整數)分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六組后,得到部分頻率分布直方圖(如圖),觀察圖形中的信息,回答下列問題.
六組后,得到部分頻率分布直方圖(如圖),觀察圖形中的信息,回答下列問題.
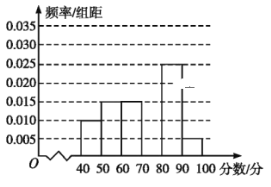
(1)求分數在![]() 內的頻率,并補全這個頻率分布直方圖;
內的頻率,并補全這個頻率分布直方圖;
(2)從頻率分布直方圖中,估計本次考試成績的眾數和平均數;
(3)若從第1組和第6組兩組學生中,隨機抽取2人,求所抽取2人成績之差的絕對值大于10的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)![]() ,g(x)
,g(x)![]() 1.
1.
(1)若f(a)=2,求實數a的值;
(2)判斷f(x)的單調性,并證明;
(3)設函數h(x)=g(x)![]() (x>0),若h(2t)+mh(t)+4>0對任意的正實數t恒成立,求實數m的取值范圍.
(x>0),若h(2t)+mh(t)+4>0對任意的正實數t恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校為了解高三年級不同性別的學生對體育課改上自習課的態度(肯定還是否定),進行了如下的調查研究.全年級共有![]() 名學生,男女生人數之比為
名學生,男女生人數之比為![]() ,現按分層抽樣方法抽取若干名學生,每人被抽到的概率均為
,現按分層抽樣方法抽取若干名學生,每人被抽到的概率均為![]() .
.
(1)求抽取的男學生人數和女學生人數;
(2)通過對被抽取的學生的問卷調查,得到如下![]() 列聯表:
列聯表:
否定 | 肯定 | 總計 | |
男生 | 10 | ||
女生 | 30 | ||
總計 |
①完成列聯表;
②能否有![]() 的把握認為態度與性別有關?
的把握認為態度與性別有關?
(3)若一班有![]() 名男生被抽到,其中
名男生被抽到,其中![]() 人持否定態度,
人持否定態度,![]() 人持肯定態度;二班有
人持肯定態度;二班有![]() 名女生被抽到,其中
名女生被抽到,其中![]() 人持否定態度,
人持否定態度,![]() 人持肯定態度.
人持肯定態度.
現從這![]() 人中隨機抽取一男一女進一步詢問所持態度的原因,求其中恰有一人持肯定態度一人持否定態度的概率.
人中隨機抽取一男一女進一步詢問所持態度的原因,求其中恰有一人持肯定態度一人持否定態度的概率.
解答時可參考下面臨界值表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若函數![]() 在
在![]() 內為增函數,求實數
內為增函數,求實數![]() 的取值范圍;
的取值范圍;
(2)若函數![]() 在
在![]() 內恰有兩個零點,求實數
內恰有兩個零點,求實數![]() 的取值范圍;
的取值范圍;
(3)已知![]() ,試估算
,試估算![]() 的近似值,(結果精確到0.001)
的近似值,(結果精確到0.001)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校象棋社團組織中國象棋比賽,采用單循環賽制,即要求每個參賽選手必須且只須和其他選手各比賽一場,勝者得![]() 分,負者得
分,負者得![]() 分,平局兩人各得
分,平局兩人各得![]() 分.若冠軍獲得者得分比其他人都多,且獲勝場次比其他人都少,則本次比賽的參賽人數至少為
分.若冠軍獲得者得分比其他人都多,且獲勝場次比其他人都少,則本次比賽的參賽人數至少為
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程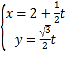 (t為參數),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為:
(t為參數),以坐標原點為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為:![]() .
.
![]() Ⅰ
Ⅰ![]() 直線l的參數方程化為極坐標方程;
直線l的參數方程化為極坐標方程;
![]() Ⅱ
Ⅱ![]() 求直線l與曲線C交點的極坐標
求直線l與曲線C交點的極坐標![]() 其中
其中![]() ,
,![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com