
���}Ŀ��ƽ���(n��i)�����c(di��n)F��0��1���Ͷ�ֱ��l��y=��1�ľ��x֮�͵���4�Ą��c(di��n)��܉�E������C���P(gu��n)������C�Ď����|(zh��)���o�������Ă��Y(ji��)Փ�� ������C�ķ��̞�x2=4y��
������C�P(gu��n)��y�S���Q
�����c(di��n)P��x��y��������C�ϣ��t|y|��2��
�����c(di��n)P������C�ϣ��t1��|PF|��4
���У��������_�Y(ji��)Փ����̖�� ��
���𰸡��ڢۢ�
���������⣺�O(sh��)P��x��y��������C�ϵ�����һ�c(di��n)�� ��?y��n)�����C��ƽ���(n��i)�����c(di��n)F��0��1��
�Ͷ�ֱ��l��y=��1�ľ��x֮�͵���4���c(di��n)��܉�E��
����|PF|+|y+1|=4���� ![]() ��
��
���y�ݩ�1�r��y=2�� ![]() x2 �� ��(d��ng)y����1�r��y=
x2 �� ��(d��ng)y����1�r��y= ![]() x2��2��
x2��2��
�@Ȼ�ٲ����_��
������C�P(gu��n)��y�S���Q�����_��
�����c(di��n)P��x��y��������C�ϣ��t|y|��2�����_��
�����c(di��n)P������C�ϣ�|PF|+|y+1|=4��|y|��2���t1��|PF|��4�����_��
���Դ��ǣ��ڢۢܣ�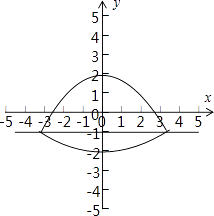


 һ�������პ(y��u)ԇ��ϵ�д�
һ�������პ(y��u)ԇ��ϵ�д� ꖹ�ԇ���Ԫ�yԇ��ϵ�д�
ꖹ�ԇ���Ԫ�yԇ��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��(sh��)��{an}��ǰn�(xi��ng)�͞�Sn �� ��Sn= ![]() nan+1 �� ����a1=1
nan+1 �� ����a1=1
��1����(sh��)��{an}��ͨ�(xi��ng)��ʽ��
��2����bn= ![]() +
+ ![]() ����(sh��)��{bn}��ǰn�(xi��ng)�͞�Tn �� ���C��Tn��2n+
����(sh��)��{bn}��ǰn�(xi��ng)�͞�Tn �� ���C��Tn��2n+ ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ��������(sh��)f��x��=3sin��2x�� ![]() ���ĈD���C���t���нY(ji��)Փ�����_����̖�� �� �وD��C�P(gu��n)��ֱ��x=
���ĈD���C���t���нY(ji��)Փ�����_����̖�� �� �وD��C�P(gu��n)��ֱ��x= ![]() ���Q��
���Q��
�ڈD��C�P(gu��n)���c(di��n)�� ![]() ��0�����Q��
��0�����Q��
�ۺ���(sh��)f��x���څ^(q��)�g���� ![]() ��
�� ![]() ����(n��i)���dž��{(di��o)�ĺ���(sh��)��
����(n��i)���dž��{(di��o)�ĺ���(sh��)��
����y=3sin2x�ĈD������ƽ�� ![]() ����λ�L�ȿ��Եõ��D��C��
����λ�L�ȿ��Եõ��D��C��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪��ABC�ă�(n��i)��A��B��C������߅�քe��a��b��c���ҝM�� ![]() =
= ![]() �� ������C��ֵ��
�� ������C��ֵ��
������ ![]() =2��b=4
=2��b=4 ![]() �����ABC����e��
�����ABC����e��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵxOy�У��AC�ķ��̞飨x+6��2+y2=25�� ����������(bi��o)ԭ�c(di��n)��O�c(di��n)��x�S�����S��O�S�����O����(bi��o)ϵ����C�ĘO����(bi��o)���̣�
����ֱ��l�ą���(sh��)���̞� ![]() ��t�酢��(sh��)��������ֱ��l�ăAб�ǣ�l�cC����A��B���c(di��n)����|AB|=
��t�酢��(sh��)��������ֱ��l�ăAб�ǣ�l�cC����A��B���c(di��n)����|AB|= ![]() ����l��б�ʣ�
����l��б�ʣ�
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����D����ֱ������ABC��A1B1C1�У���BAC=90�㣬AC=2 ![]() ��AA1=
��AA1= ![]() ��AB=2���c(di��n)D����B1C1�ϣ���B1C1=4B1D �������C��BD��A1C
��AB=2���c(di��n)D����B1C1�ϣ���B1C1=4B1D �������C��BD��A1C
����������B��A1D��C�Ĵ�С��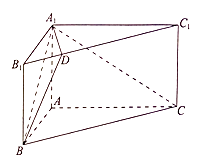
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ���C���}��
��1����֪�AC�ĈA����x��y+1=0�cx�S�Ľ��c(di��n)�����cֱ��x+y+3=0���У���AC�Ę�(bi��o)��(zh��n)���̣�
��2�����c(di��n)P��x��y���ڈAx2+y2��4y+3=0�ϣ��� ![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ�����H�̓r��ijһ�r�g��(n��i)�ʬF(xi��n)�����Ҳ���Ҏ(gu��)�ɣ�P=Asin���ئ�t+ ![]() ��+60����Ԫ��[t���죩��A��0���أ�0]���F(xi��n)�ɼ���������Ϣ������̓r80��Ԫ����(d��ng)t=150���죩�r�_(d��)������̓r���t��= ��
��+60����Ԫ��[t���죩��A��0���أ�0]���F(xi��n)�ɼ���������Ϣ������̓r80��Ԫ����(d��ng)t=150���죩�r�_(d��)������̓r���t��= ��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
���}Ŀ����֪���l���غϵ�ֱ�� ![]() �̓ɂ����غϵ�ƽ��
�̓ɂ����غϵ�ƽ�� ![]() ���������}���_���ǣ� ��
���������}���_���ǣ� ��
A.�� ![]() ��
�� ![]() ���t
���t ![]()
B.�� ![]() ��
�� ![]() ����
���� ![]() ���t
���t ![]()
C.�� ![]() ��
�� ![]() ���t
���t ![]()
D.�� ![]() ��
�� ![]() ����
���� ![]() ���t
���t ![]()
�鿴�𰸺ͽ���>>
���H�W(xu��)У��(y��u)�x - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_ | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com