【題目】已知函數
（
）．
（1）若函數
在
上單調遞減，求實數
的取值范圍；
（2）當
時，試問方程
是否有實數根？若有，求出所有實數根；若沒有，請說明理由．
【答案】(1) 
(2) 沒有實數根
【解析】試題分析：（1）求出函數
的導數
，設
，根據函數
在
上單調遞減，可得
在
上小于等于0恒成立，從而可得
，即可得到實數
的取值范圍；（2）當
時， 
，整理得
，設
，利用單調性求得
；設
，利用單調性求得
，根據
與
在不同的
值處取得，即可得到方程無實根．
試題解析：（1）由題知， 
，設
，
∵函數
在
上單調遞減
∴
在
上小于等于0恒成立.
∴
解得
∴實數
的取值范圍為
．
（2）沒有實數根．
當
時， 
，整理得
.
設
，則
，
當
時， 
，則
在
上單調遞減；
當
時， 
，則
在
上單調遞增.
∴
．
設
，則
，
當
時， 
，則
在
上單調遞增；
當
時， 
，則
在
上單調遞減，
∴
，
∵
與
在不同的
值處取得
∴根據函數圖象可知
恒成立
∴方程無實根．
科目：高中數學 來源： 題型：
【題目】心理學家發現視覺和空間能力與性別有關,某數學興趣小組為了驗證這個結論,從興趣小組中按分層抽樣的方法抽取50名同學,給所有同學幾何和代數各一題,讓各位同學自由選擇一道題進行解答.統計情況如下表:(單位:人)
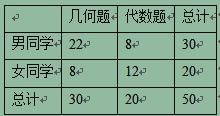
(1)能否據此判斷有
的把握認為視覺和空間能力與性別有關?
(2)經過多次測試發現:女生甲解答一道幾何題所用的時間在5—7分鐘,女生乙解答一道幾何題所用的時間在6—8分鐘,現甲、乙兩人獨立解答同一道幾何題,求乙比甲先解答完的概率;
(3)現從選擇幾何題的8名女生中任意抽取兩人對她們的答題情況進行研究,記甲、乙兩名女生被抽到的人數為
,求
的分布列及數學期望.
附表及公式
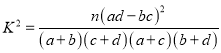
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝xlnx和g(x)＝m(x2－1)(m∈R)．
(1)m＝1時，求方程f(x)＝g(x)的實根；
(2)若對任意的x∈(1，＋∞)，函數y＝g(x)的圖象總在函數y＝f(x)圖象的上方，求m的取值范圍；
(3)求證： 
＋
＋…＋
>ln(2n＋1) (n∈N*)．
查看答案和解析>>
科目：高中數學 來源： 題型：
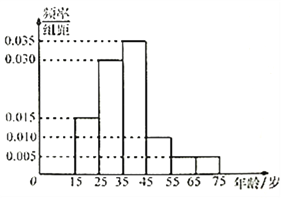
【題目】2017年5月14日,第一屆“一帶一路”國際高峰論壇在北京舉行,為了解不同年齡的人對“一帶一路”關注程度,某機構隨機抽取了年齡在
歲之間的100人進行調查,并按年齡繪制成頻率分布直方圖,如圖所示,其分組區間為: 
, 
,
,
,
,
.把年齡落在區間
和
內的人分別稱為“青少年”和“中老年”.
(1)根據頻率分布直方圖求樣本的中位數(保留兩位小數)和眾數
(2)根據已知條件完成下面的2×2列聯表,并判斷能否有99%的把握認為關注“帶一路”是否和年齡段有關?
關注 | 不關注 | 合計 | |
青少年 | 15 | ||
中老年 | |||
合計 | 50 | 50 | 100 |
附:參考公式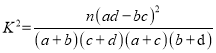
，其中
臨界值表：
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】2017年5月14日,第一屆“一帶一路”國際高峰論壇在北京舉行,為了解不同年齡的人對“一帶一路”關注程度,某機構隨機抽取了年齡在15-75歲之間的100人進行調查, 經統計“青少年”與“中老年”的人數之比為9:11
關注 | 不關注 | 合計 | |
青少年 | 15 | ||
中老年 | |||
合計 | 50 | 50 | 100 |
(1)根據已知條件完成上面的
列聯表，并判斷能否有
的把握認為關注“一帶一路”是否和年齡段有關？
(2)現從抽取的青少年中采用分層抽樣的辦法選取9人進行問卷調查.在這9人中再選取3人進行面對面詢問,記選取的3人中關注“一帶一路”的人數為X,求X的分布列及數學期望.
附:參考公式
，其中
臨界值表：
| 0.05 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某超市在2017年五一正式開業，開業期間舉行開業大酬賓活動，規定：一次購買總額在區間
內者可以參與一次抽獎，根據統計發現參與一次抽獎的顧客每次購買金額分布情況如下：
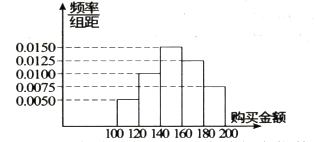
（1）求參與一次抽獎的顧客購買金額的平均數與中位數（同一組中的數據用該組區間的中點值作代表，結果保留到整數）；
（2）若根據超市的經營規律，購買金額
與平均利潤
有以下四組數據：
試根據所給數據，建立
關于
的線性回歸方程
，并根據（1）中計算的結果估計超市對每位顧客所得的利潤.
參考公式：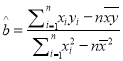 
， 
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
:
的一個焦點與拋物線
的焦點重合，且過點
.過點
的直線
交橢圓
于
， 
兩點， 
為橢圓的左頂點.
(Ⅰ)求橢圓
的標準方程；
(Ⅱ)求
面積的最大值，并求此時直線
的方程.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
