解:(1)由題意可得 φ(x)=a
2 (x-1)
2 ,值域為[0,+∞). …(2分)
(2)不等式(x-1)
2>f(x)的解集中的整數恰有3個,
等價于(1-a
2) x
2-2x+1>0 恰有三個整數解,故 1-a
2<0,即 a>1,∴(1-a
2) x
2-2x+1=[((1-a)x-1][(1+a)x-1]>0,
所以
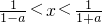
,又因為
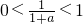
,
所以

,解之得
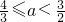
. …(6分)
(3)設F(x)=f(x)-g(x)=

x
2-elnx,則 F′(x)=x-
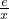
=
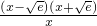
.
所以當 0<x<

時,F′(x)>0;當 x>

時,F′(x)<0.
因此 x=

時,F(x) 取得最小值0,
則 f(x)與g(x)的圖象在x=

處有公共點 (

,

). …(8分)
設f(x)與g(x)存在“分界線”,方程為 y-

=k(x-

),即 y=kx+

-k

,
由 f(x)≥kx+

-k

,對x∈R恒成立,
則 x
2-2kx-e+2k

≥0 在x∈R恒成立.
所以△=4k
2-4(2k

-e)=4
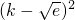
≤0成立,因此 k=

.…(10分)
下面證明 g(x)≤
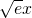
-

(x>0)恒成立.
設G(x)=elnx-x

+

,則 G′(x)=
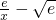
=
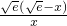
.
所以當 0<x<

時,G′(x)>0;當 x>

時,G′(x)<0.
因此 x=

時,G(x)取得最大值0,則 g(x)≤
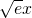
-

(x>0)成立.
故所求“分界線”方程為:y=
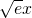
-

. …(14分)
分析:(1)由函數圖象的變換可得 φ(x)=a
2 (x-1)
2 ,值域為[0,+∞).
(2)由題意可得(1-a
2) x
2-2x+1>0 恰有三個整數解,故 1-a
2<0,再由(1-a
2) x
2-2x+1>0,求得實數a的取值范圍.
(3)設F(x)=f(x)-g(x)=

x
2-elnx,利用導數知識判斷單調性,求出 x=

時,F(x) 取得最小值0.設f(x)與g(x)存在“分界線”,方程為 y=kx+

-k

,由 f(x)≥kx+

-k

,對x∈R恒成立,求得k=

.再利用導數證明g(x)≤
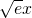
-

(x>0)恒成立,從而得到所求“分界線”方程.
點評:本題主要考查平移,值域,解整式和分式不等式,切線方程的求法,導數知識判斷單調性及其應用,存在性,以及探索、等價轉化和推理證明能力,解決綜合問題的能力.

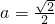 ,b=e,試探究f(x)與g(x)是否存在“分界線”?若存在,求出“分界線”的方程;若不存在,請說明理由.
,b=e,試探究f(x)與g(x)是否存在“分界線”?若存在,求出“分界線”的方程;若不存在,請說明理由.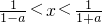 ,又因為
,又因為 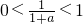 ,
, ,解之得
,解之得 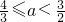 . …(6分)
. …(6分) x2-elnx,則 F′(x)=x-
x2-elnx,則 F′(x)=x-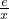 =
=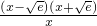 .
. 時,F′(x)>0;當 x>
時,F′(x)>0;當 x> 時,F′(x)<0.
時,F′(x)<0. 時,F(x) 取得最小值0,
時,F(x) 取得最小值0, 處有公共點 (
處有公共點 ( ,
, ). …(8分)
). …(8分) =k(x-
=k(x- ),即 y=kx+
),即 y=kx+ -k
-k ,
, -k
-k ,對x∈R恒成立,
,對x∈R恒成立, ≥0 在x∈R恒成立.
≥0 在x∈R恒成立. -e)=4
-e)=4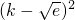 ≤0成立,因此 k=
≤0成立,因此 k= .…(10分)
.…(10分)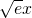 -
- (x>0)恒成立.
(x>0)恒成立. +
+ ,則 G′(x)=
,則 G′(x)=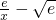 =
=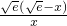 .
. 時,G′(x)>0;當 x>
時,G′(x)>0;當 x> 時,G′(x)<0.
時,G′(x)<0. 時,G(x)取得最大值0,則 g(x)≤
時,G(x)取得最大值0,則 g(x)≤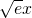 -
- (x>0)成立.
(x>0)成立.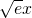 -
- . …(14分)
. …(14分) x2-elnx,利用導數知識判斷單調性,求出 x=
x2-elnx,利用導數知識判斷單調性,求出 x= 時,F(x) 取得最小值0.設f(x)與g(x)存在“分界線”,方程為 y=kx+
時,F(x) 取得最小值0.設f(x)與g(x)存在“分界線”,方程為 y=kx+ -k
-k ,由 f(x)≥kx+
,由 f(x)≥kx+ -k
-k ,對x∈R恒成立,求得k=
,對x∈R恒成立,求得k= .再利用導數證明g(x)≤
.再利用導數證明g(x)≤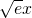 -
- (x>0)恒成立,從而得到所求“分界線”方程.
(x>0)恒成立,從而得到所求“分界線”方程.

 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案