【題目】2017年11月、12月全國大范圍流感爆發，為研究晝夜溫差大小與患感冒人數多少之間的關系，一興趣小組抄錄了某醫院11月到12月間的連續6個星期的晝夜溫差情況與因患感冒而就診的人數，得到如下資料:
日期 | 第一周 | 第二周 | 第三周 | 第四周 | 第五周 | 第六周 |
晝夜溫差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
就診人數y(個) | 22 | 25 | 29 | 26 | 16 | 12 |
該興趣小組確定的研究方案是：先從這六組數據中選取2組，用剩下的4組數據求線性回歸方程，再用被選取的2組數據進行檢驗。
(Ⅰ)求選取的2組數據恰好是相鄰兩個星期的概率；
(Ⅱ)若選取的是第一周與第六周的兩組數據，請根據第二周到第五周的4組數據,求出
關于
的線性回歸方程
；
(Ⅲ)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2人,則認為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?
(參考公式: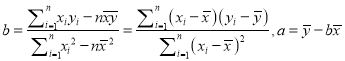 
)
參考數據： 
1092， 
498
【答案】(Ⅰ) 
;(Ⅱ)見解析;(Ⅲ)見解析.
【解析】試題分析：(Ⅰ)用列舉法列出所有的基本事件，再找出相鄰兩個星期的數據的事件個數，利用古典概型的概率公式即可求得；(Ⅱ)根據所給數據分別算出
， 
，再根據求線性回歸方程系數的方法求得
，把
， 
和
代入到求
得公式，求出
，即可求出線性回歸方程；(Ⅲ)根據所求的線性回歸方程，將
和
代入求得
，再同原來表中所給的
和
對應的值做差，差的絕對值不超過
，即可得到線性回歸方程理想．
試題解析：(Ⅰ)將連續六組數據分別記為
，從六組中任意選取兩組，其基本事件為： 
，共15種情況.
其中兩組是相鄰的為
，共5種情況.
設抽到相鄰兩個星期的數據為事件
，則抽到相鄰兩個星期的數據的概率為
.
(Ⅱ)由數據求得
，由公式求得
，再由
.
∴
關于
的線性回歸方程為
(Ⅲ)當
時, 
, 
；
同樣, 當
時, 
, 
.
∴該小組所得線性回歸方程是理想的
全能測控期末小狀元系列答案科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，拋物線
的頂點在原點，且該拋物線經過點
，其焦點
在
軸上.
（Ⅰ）求過點且與直線
垂直的直線的方程；
（Ⅱ）設過點
的直線交拋物線于
，
兩點，
，求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知
為實數，用
表示不超過的最大整數.
（1）若函數
，求
的值；
（2）若函數
，求
的值域；
（3）若存在
且
，使得
，則稱函數是
函數，若函數 
是函數，求
的取值范圍.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在平面直角坐標系
中，點
在橢圓
：
上，且橢圓的離心率為
.
(1)求橢圓的標準方程；
(2)記橢圓的左、右頂點分別為
、
,點
是
軸上任意一點(異于點
)，過點的直線
與橢圓相交于
兩點.
①若點的坐標為
，直線
的斜率為
，求
的面積;
②若點的坐標為
，連結
交于點
，記直線
的斜率分別為
，證明：
是定值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】空氣質量指數（簡稱：
）是定量描述空氣質量狀況的無量綱指數，空氣質量按照大小分為六級：
為優，
為良，
為輕度污染，
為中度污染，
為重度污染，
為嚴重污染.下面記錄了北京市
天的空氣質量指數，根據圖表，下列結論錯誤的是（ ）
A. 在北京這天的空氣質量中，按平均數來考察，最后
天的空氣質量優于最前面天的空氣質量 B. 在北京這天的空氣質量中，有
天達到污染程度
C. 在北京這天的空氣質量中，12月29日空氣質量最好 D. 在北京這天的空氣質量中，達到空氣質量優的天數有
天
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列結論：
(1)某學校從編號依次為001，002，…，900的900個學生中用系統抽樣的方法抽取一個樣本，已知樣本中有兩個相鄰的編號分別為053，098，則樣本中最大的編號為862.
(2)甲組數據的方差為5，乙組數據為5、6、9、10、5，那么這兩組數據中較穩定的是甲.
(3)若兩個變量的線性相關性越強，則相關系數
的值越接近于1.
(4)對A、B、C三種個體按3:1:2的比例進行分層抽樣調查，若抽取的A種個體有15個，則樣本容量為30.
則正確的個數是
A. 3 B. 2 C. 1 D. 0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
