【題目】根據以往的經驗，某建筑工程施工期間的降水量
（單位：
）對工期的影響如下表：
降水量 |
|
|
|
|
工期延誤天數 | 0 | 1 | 3 | 6 |
根據某氣象站的資料，某調查小組抄錄了該工程施工地某月前
天的降水量的數據，繪制得到降水量的折線圖，如下圖所示.
（1）求這天的平均降水量；
（2）根據降水量的折線圖，分別估計該工程施工延誤天數
的概率.
科目：高中數學 來源： 題型：
【題目】絕對值|x﹣1|的幾何意義是數軸上的點x與點1之間的距離，那么對于實數a，b，
的幾何意義即為點x與點a、點b的距離之和.
（1）直接寫出
與
的最小值，并寫出取到最小值時x滿足的條件；
（2）設a1≤a2≤…≤an是給定的n個實數，記S=
.試猜想：若n為奇數，則當x∈ 時S取到最小值；若n為偶數，則當x∈ 時，S取到最小值；（直接寫出結果即可）
（3）求
的最小值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在極坐標系中，曲線
，
，C與l有且僅有一個公共點．
（Ⅰ）求a；
（Ⅱ）O為極點，A，B為C上的兩點，且
，求
的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設
為常數，函數
，給出以下結論：
（1）若
，則
存在唯一零點
（2）若
，則
（3）若有兩個極值點
，則
其中正確結論的個數是（ ）
A. 3B. 2C. 1D. 0
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某學校在九年級上學期開始時要掌握全年級學生每分鐘跳繩的情況，隨機抽取了100名學生進行測試，得到頻率分布直方圖（如圖），且規定計分規則如下表：
每分鐘跳繩個數 |
|
|
|
|
得分 | 17 | 18 | 19 | 20 |
（1）請估計學生的跳繩個數的眾數和平均數（保留整數）；
（2）若從跳繩個數在
，
兩組中按分層抽樣的方法抽取9人參加正式測試，并從中任意選取2人，求2人得分之和不大于34分的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】根據以往的經驗，某建筑工程施工期間的降水量
（單位：
）對工期的影響如下表：
降水量 |
|
|
|
|
工期延誤天數 | 0 | 1 | 3 | 6 |
根據某氣象站的資料，某調查小組抄錄了該工程施工地某月前
天的降水量的數據，繪制得到降水量的折線圖，如下圖所示.
（1）根據降水量的折線圖，分別求該工程施工延誤天數
的頻率；
（2）以（1）中的頻率作為概率，求工期延誤天數
的分布列及數學期望與方差.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖1,在正方形
中，
是
的中點，點
在線段
上,且
.若將
分別沿
折起，使
兩點重合于點
,如圖2.
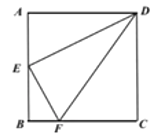
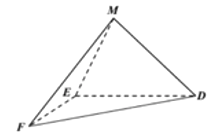
圖1 圖2
(1)求證:
平面
；
(2)求直線
與平面
所成角的正弦值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知f（x）是R上的奇函數，且x>0時，f（x）=x2-4x+3．
求：（1）f（x）的解析式．
（2）已知t＞0，求函數f（x）在區間[t，t+1]上的最小值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
