
【題目】某市醫療保險實行定點醫療制度,按照“就近就醫、方便管理”的原則,參加保險人員可自主選擇四家醫療保險定點醫院和一家社區醫院作為本人就診的醫療機構.若甲、乙、丙、丁4名參加保險人員所在地區附近有A,B,C三家社區醫院,并且他們的選擇是相互獨立的.
(Ⅰ)求甲、乙兩人都選擇A社區醫院的概率;
(Ⅱ)求甲、乙兩人不選擇同一家社區醫院的概率;
(Ⅲ)設4名參加保險人員中選擇A社區醫院的人數為ξ,求ξ的分布列和數學期望.
【答案】解:(Ⅰ)設“甲、乙兩人都選擇A社區醫院”為事件A,那么P(A)= ![]() ×
× ![]() =
= ![]() 所以甲、乙兩人都選擇A社區醫院的概率為
所以甲、乙兩人都選擇A社區醫院的概率為 ![]() .
.
(Ⅱ)設“甲、乙兩人選擇同一個社區醫院”為事件B,
由于有A,B,C三家社區醫院,所以P(B)=3× ![]() ×
× ![]() =
= ![]()
所以甲、乙兩人不選擇同一個社區醫院的概率是P( ![]() )=1﹣P(B)=
)=1﹣P(B)= ![]() .
.
(Ⅲ)隨機變量ξ可能取的值為0,1,2,3,4.那么
P(ξ=0)= ![]() =
= ![]() ; P(ξ=1)=
; P(ξ=1)= ![]() =
= ![]() ;
;
P(ξ=2)= ![]() =
= ![]() ;P(ξ=3)=
;P(ξ=3)= ![]() =
= ![]() ;P(ξ=4)=
;P(ξ=4)= ![]() =
= ![]()
所以ξ的分布列為
ξ | 0 | 1 | 2 | 3 | 4 |
P |
|
|
|
|
|
Eξ=0× ![]() +1×
+1× ![]() +2×
+2× ![]() +3×
+3× ![]() +4×
+4× ![]() =
= ![]()
【解析】(Ⅰ)設“甲、乙兩人都選擇A社區醫院”為事件A,由于他們的選擇是相互獨立,故利用乘法公式可求;(Ⅱ)先求甲、乙兩人選擇同一個社區醫院的事件的概率,再求甲、乙兩人不選擇同一個社區醫院的概率;(Ⅲ)確定隨機變量ξ可能取的值,計算相應的概率,即可得到ξ的分布列與數學期望.


 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:高中數學 來源: 題型:
【題目】正三棱臺的上、下底面的邊長分別是3和6. 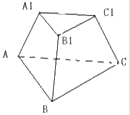
(1)若側面與底面所成的角為60°,求此三棱臺的體積;
(2)若側棱與底面所成的角為60°,求此三棱臺的側面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)當![]() 時,若函數
時,若函數![]() 的導函數
的導函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() ,
, ![]() 兩點,其橫坐標分別為
兩點,其橫坐標分別為![]() ,
, ![]() ,線段
,線段![]() 的中點的橫坐標為
的中點的橫坐標為![]() ,且
,且![]() ,
, ![]() 恰為函數
恰為函數![]() 的零點,求證:
的零點,求證: ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)= 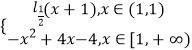
(1)在給定直角坐標系內直接畫出f(x)的草圖(不用列表描點),并由圖象寫出函數 f(x)的單調減區間; 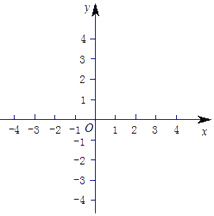
(2)當m為何值時f(x)+m=0有三個不同的零點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】銷售甲、乙兩種商品所得利潤分別是y1 , y2萬元,它們與投入資金x萬元的關系分別為y1=m ![]() +a,y2=bx,(其中m,a,b都為常數),函數y1 , y2對應的曲線C1 , C2如圖所示.
+a,y2=bx,(其中m,a,b都為常數),函數y1 , y2對應的曲線C1 , C2如圖所示. 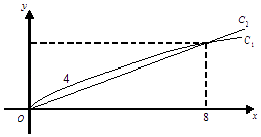
(1)求函數y1與y2的解析式;
(2)若該商場一共投資10萬元經銷甲、乙兩種商品,求該商場所獲利潤的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)是(﹣∞,0)∪(0,+∞)上的奇函數,且當x<0時,函數的部分圖象如圖所示,則不等式xf(x)<0的解集是( ) 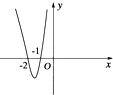
A.(﹣2,﹣1)∪(1,2)
B.(﹣2,﹣1)∪(0,1)∪(2,+∞)
C.(﹣∞,﹣2)∪(﹣1,0)∪(1,2)
D.(﹣∞,﹣2)∪(﹣1,0)∪(0,1)∪(2,+∞)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,且過點
,且過點 .
.
(1)求![]() 的方程;
的方程;
(2)是否存在直線![]() 與
與![]() 相交于
相交于![]() 兩點,且滿足:①
兩點,且滿足:①![]() 與
與![]() (
(![]() 為坐標原點)的斜率之和為2;②直線
為坐標原點)的斜率之和為2;②直線![]() 與圓
與圓![]() 相切,若存在,求出
相切,若存在,求出![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了響應教育部頒布的《關于推進中小學生研學旅行的意見》,某校計劃開設八門研學旅行課程,并對全校學生的選課意向進行調查(調查要求全員參與,每個學生必須從八門課程中選出唯一一門課程).本次調查結果如下.
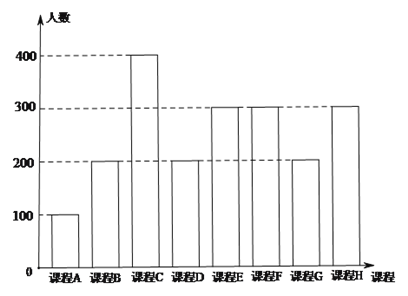
圖中,課程![]() 為人文類課程,課程
為人文類課程,課程![]() 為自然科學類課程.為進一步研究學生選課意向,結合上面圖表,采取分層抽樣方法從全校抽取1%的學生作為研究樣本組(以下簡稱“組
為自然科學類課程.為進一步研究學生選課意向,結合上面圖表,采取分層抽樣方法從全校抽取1%的學生作為研究樣本組(以下簡稱“組![]() ”).
”).
(Ⅰ)在“組![]() ”中,選擇人文類課程和自然科學類課程的人數各有多少?
”中,選擇人文類課程和自然科學類課程的人數各有多少?
(Ⅱ)某地舉辦自然科學營活動,學校要求:參加活動的學生只能是“組![]() ”中選擇
”中選擇![]() 課
課
程或![]() 課程的同學,并且這些同學以自愿報名繳費的方式參加活動. 選擇
課程的同學,并且這些同學以自愿報名繳費的方式參加活動. 選擇![]() 課程的學生中有
課程的學生中有![]() 人參加科學營活動,每人需繳納
人參加科學營活動,每人需繳納![]() 元,選擇
元,選擇![]() 課程的學生中有
課程的學生中有![]() 人參加該活動,每人需繳納
人參加該活動,每人需繳納![]() 元.記選擇
元.記選擇![]() 課程和
課程和![]() 課程的學生自愿報名人數的情況為
課程的學生自愿報名人數的情況為![]() ,參加活動的學生繳納費用總和為
,參加活動的學生繳納費用總和為![]() 元.
元.
①當![]() 時,寫出
時,寫出![]() 的所有可能取值;
的所有可能取值;
②若選擇![]() 課程的同學都參加科學營活動,求
課程的同學都參加科學營活動,求![]() 元的概率.
元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
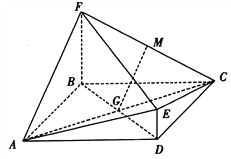
【題目】如圖,菱![]() 與四邊形BDEF相交于BD,
與四邊形BDEF相交于BD, ![]() 平面ABCD,DE//BF,BF=2DE,AF⊥FC,M為CF的中點,
平面ABCD,DE//BF,BF=2DE,AF⊥FC,M為CF的中點, ![]() .
.
(I)求證:GM//平面CDE;
(II)求證:平面ACE⊥平面ACF.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com