【題目】平面
以任意角度截正方體，所截得的截面圖形可以是_____
填上所有你認為正確的序號
正三邊形 
正四邊形 
正五邊形 
正六邊形 
鈍角三角形 
等腰梯形 
非矩形的平行四邊形
【答案】
【解析】
正方體有六個面，用平面去截正方體時最多與六個面相交得正六邊形，最少與三個面相交得正三邊形，因此用一個平面去截一正方體，截面可能為正三邊形，正四邊形，正六邊形，等腰梯形，非矩形的平行四邊形．
解：畫出截面圖形如圖：
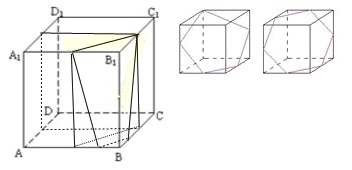
可以畫出三邊形，但不能畫出直角三角形和鈍角三角形，故
正確，
錯誤；
可以畫出正四邊形，故
正確；
經過正方體的一個頂點去切就可得到五邊形
但此時不可能是正五邊形，故
錯誤；．
正方體有六個面，用平面去截正方體時最多與六個面相交得六邊形，且可以畫出正六邊形，故
正確；
可以畫出梯形但不是直角梯形，故
正確．
可以畫出非矩形的平行四邊形，故
．
故平面
以任意角度截正方體，所截得的截面圖形可以是：正三邊形，正四邊形，正六邊形，等腰梯形，非矩形的平行四邊形．
故答案為：．
步步高達標卷系列答案科目：高中數學 來源： 題型：
【題目】給定下列四個命題：
若一個平面內的兩條直線與另一個平面都平行，那么這兩個平面相互平行；
若一個平面經過另一個平面的垂線，那么這兩個平面相互垂直；
垂直于同一直線的兩條直線相互平行；
若兩個平面垂直，那么一個平面內與它們的交線不垂直的直線與另一個平面也不垂直．
其中，為真命題的是
A. 和 B. 和 C. 和 D. 和
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以直角坐標系的原點
為極點，
軸的正半軸為極軸，且兩個坐標系取相等的長度單位建立坐標系.已知直線
的極坐標方程為
，曲線
的參數方程為
（
為參數）.
（1）求曲線的普通方程和直線的直角坐標方程；
（2）直線上有一點
，設直線與曲線相交于
兩點，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】對于函數
，若在其定義域內存在實數
，使得
成立，則稱有“※點”。
（1）判斷函數
在
上是否有“※點”。并說明理由；
（2）若函數
在
上有“※點”，求正實數a的取值范圍。
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（10分）四面體ABCD及其三視圖如圖所示，平行于棱AD，BC的平面分別交四面體的棱AB，BD，DC，CA于點E，F，G，H．
（1）求四面體ABCD的體積；
（2）證明：四邊形EFGH是矩形．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在四棱錐P﹣ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD=DC=AP=2，AB=1，點E為棱PC的中點．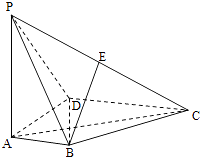 
（1）證明：BE⊥DC；
（2）求直線BE與平面PBD所成角的正弦值；
（3）若F為棱PC上一點，滿足BF⊥AC，求二面角F﹣AB﹣P的余弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】給出下列命題：
①存在實數
,使
； ②函數
是偶函數；
③若
是第一象限的角，且
，則
；
④直線
是函數
的一條對稱軸；
⑤函數
的圖像關于點
成對稱中心圖形.
其中正確命題的序號是__________.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】中國南北朝時期的著作《孫子算經》中，對同余除法有較深的研究．設
為整數，若
和
被
除得的余數相同，則稱和對模同余，記為
．若
，
，則的值可以是
A. 2015 B. 2016 C. 2017 D. 2018
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
