
【題目】在平面直角坐標(biāo)平面中, ![]() 的兩個頂點為
的兩個頂點為![]() ,平面內(nèi)兩點
,平面內(nèi)兩點![]() 、
、![]() 同時滿足:①
同時滿足:①![]() ;②
;②![]() ;③
;③![]() .
.
(1)求頂點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)過點![]() 作兩條互相垂直的直線
作兩條互相垂直的直線![]() ,直線
,直線![]() 與點
與點![]() 的軌跡
的軌跡![]() 相交弦分別為
相交弦分別為![]() ,設(shè)弦
,設(shè)弦![]() 的中點分別為
的中點分別為![]() .
.
①求四邊形![]() 的面積
的面積![]() 的最小值;
的最小值;
②試問:直線![]() 是否恒過一個定點?若過定點,請求出該定點,若不過定點,請說明理由.
是否恒過一個定點?若過定點,請求出該定點,若不過定點,請說明理由.
【答案】(1)![]() ;(2)①
;(2)①![]() 的最小值的
的最小值的![]() ,②直線
,②直線![]() 恒過定點
恒過定點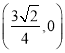 .
.
【解析】試題分析:(1)由![]() 可得
可得![]() 為
為![]() 的重心,設(shè)
的重心,設(shè)![]() ,則
,則![]() ,再由
,再由![]() ,可得
,可得![]() 為
為![]() 的外心,
的外心, ![]() 在
在![]() 軸上,再由
軸上,再由![]() ∥
∥![]() ,可得
,可得![]() ,結(jié)合
,結(jié)合![]() 即可求得頂點
即可求得頂點![]() 的軌跡
的軌跡![]() 的方程;(2)
的方程;(2)![]() 恰為
恰為![]() 的右焦點.當(dāng)直線
的右焦點.當(dāng)直線![]() ,
, ![]() 的斜率存在且不為0時,設(shè)直線
的斜率存在且不為0時,設(shè)直線![]() 的方程為
的方程為![]() .聯(lián)立直線方程與橢圓方程,化為關(guān)于
.聯(lián)立直線方程與橢圓方程,化為關(guān)于![]() 的一元二次方程,利用根與系數(shù)的關(guān)系求得
的一元二次方程,利用根與系數(shù)的關(guān)系求得![]() 的縱坐標(biāo)得到和與積.①根據(jù)焦半徑公式得
的縱坐標(biāo)得到和與積.①根據(jù)焦半徑公式得![]() 、
、![]() ,代入四邊形面積公式,再由基本不等式求得四邊形
,代入四邊形面積公式,再由基本不等式求得四邊形![]() 面積
面積![]() 的最小值;②根據(jù)中點坐標(biāo)公式得
的最小值;②根據(jù)中點坐標(biāo)公式得![]() 的坐標(biāo),得到直線
的坐標(biāo),得到直線![]() 的方程,化簡整理令
的方程,化簡整理令![]() 解得
解得![]() 值,可得直線
值,可得直線![]() 恒過定點;當(dāng)直線
恒過定點;當(dāng)直線![]() ,
, ![]() 有一條直線的斜率不存在時,另一條直線的斜率為0,直線
有一條直線的斜率不存在時,另一條直線的斜率為0,直線![]() 即為
即為![]() 軸,過點(
軸,過點(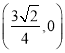 .
.
試題解析:(1)∵![]()
∴由①知![]()
∴![]() 為
為![]() 的重心
的重心
設(shè)![]() ,則
,則![]() ,由②知
,由②知![]() 是
是![]() 的外心
的外心
∴![]() 在
在![]() 軸上由③知
軸上由③知![]() ,由
,由![]() ,得
,得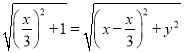 ,化簡整理得:
,化簡整理得: ![]() .
.
(2)解: ![]() 恰為
恰為![]() 的右焦點,
的右焦點,
①當(dāng)直線![]() 的斜率存且不為0時,設(shè)直線
的斜率存且不為0時,設(shè)直線![]() 的方程為
的方程為![]() ,
,
由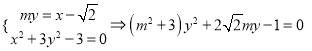 ,
,
設(shè)![]() 則
則![]() ,
,
①根據(jù)焦半徑公式得![]() ,
,
又![]() ,
,
所以 ,同理
,同理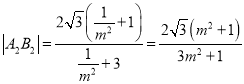 ,
,
則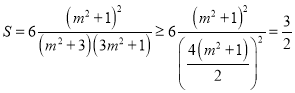 ,
,
當(dāng)![]() ,即
,即![]() 時取等號.
時取等號.
②根據(jù)中點坐標(biāo)公式得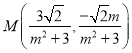 ,同理可求得
,同理可求得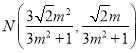 ,
,
則直線![]() 的斜率為
的斜率為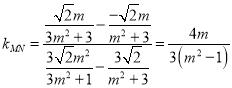 ,
,
∴直線![]() 的方程為
的方程為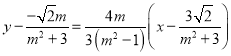 ,
,
整理化簡得![]() ,
,
令![]() ,解得
,解得![]()
∴直線![]() 恒過定點
恒過定點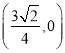 ,
,
②當(dāng)直線![]() 有一條直線斜率不存在時,另一條斜率一定為0,直線
有一條直線斜率不存在時,另一條斜率一定為0,直線![]() 即為
即為![]() 軸,過點
軸,過點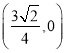 ,
,
綜上, ![]() 的最小值的
的最小值的![]() ,直線
,直線![]() 恒過定點
恒過定點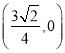 .
.


 發(fā)散思維新課堂系列答案
發(fā)散思維新課堂系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() )
)
(1)討論![]() 的單調(diào)性;
的單調(diào)性;
(2)設(shè)![]() ,若
,若![]() 有兩個極值點
有兩個極值點![]() ,且不等式
,且不等式![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知公差大于零的等差數(shù)列{an}的前n項和為Sn , 且滿足a3a4=117,a2+a5=22.
(1)求通項an;
(2)若數(shù)列{bn}滿足bn= ![]() ,是否存在非零實數(shù)c使得{bn}為等差數(shù)列?若存在,求出c的值;若不存在,請說明理由.
,是否存在非零實數(shù)c使得{bn}為等差數(shù)列?若存在,求出c的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在一條生產(chǎn)線上按同樣的方式每隔30分鐘取一件產(chǎn)品,共取了n件,測得其產(chǎn)品尺寸后,畫得其頻率分布直方圖如圖所示,已知尺寸在[15,45)內(nèi)的頻數(shù)為46. 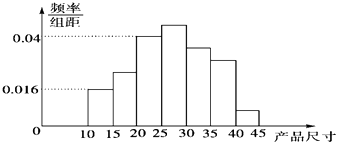
(1)該抽樣方法是什么方法?
(2)求n的值;
(3)求尺寸在[20,25)內(nèi)的產(chǎn)品的件數(shù).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在平面直角坐標(biāo)系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() ,
, ![]() 為參數(shù)),在以
為參數(shù)),在以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸的極坐標(biāo)系中,曲線
軸的正半軸為極軸的極坐標(biāo)系中,曲線![]() 是圓心在極軸上,且經(jīng)過極點的圓.已知曲線
是圓心在極軸上,且經(jīng)過極點的圓.已知曲線![]() 上的點
上的點 對應(yīng)的參數(shù)
對應(yīng)的參數(shù)![]() ,射線
,射線![]() 與曲線
與曲線![]() 交于點
交于點![]() .
.
(Ⅰ)求曲線![]() 的直角坐標(biāo)方程;
的直角坐標(biāo)方程;
(Ⅱ)若點![]() ,
, ![]() 在曲線
在曲線![]() 上,求
上,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某市出租車的計價標(biāo)準(zhǔn)是:4km以內(nèi)(含4km)10元,超過4km且不超過18km的部分1.2元/km,超過18km的部分1.8元/km,不計等待時間的費用.
(1)如果某人乘車行駛了10km,他要付多少車費?
(2)試建立車費y(元)與行車?yán)锍蘹(km)的函數(shù)關(guān)系式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)f(x)=![]()
(1)證明f(x)是奇函數(shù);
(2)判斷f(x)的單調(diào)性,并用定義證明
(3)求f(x)在[1,2]上的最值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】選修4-4:坐標(biāo)系與參數(shù)方程
在直角坐標(biāo)系![]() 中,以
中,以![]() 為極點,
為極點, ![]() 軸正半軸為極軸建立極坐標(biāo)系,直線
軸正半軸為極軸建立極坐標(biāo)系,直線![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為![]() (
(![]() ),
),![]() 為
為![]() 上一點,以
上一點,以![]() 為邊作等邊三角形
為邊作等邊三角形![]() ,且
,且![]() 、
、![]() 、
、![]() 三點按逆時針方向排列.
三點按逆時針方向排列.
(Ⅰ)當(dāng)點![]() 在
在![]() 上運動時,求點
上運動時,求點![]() 運動軌跡的直角坐標(biāo)方程;
運動軌跡的直角坐標(biāo)方程;
(Ⅱ)若曲線![]() :
: ![]() ,經(jīng)過伸縮變換
,經(jīng)過伸縮變換![]() 得到曲線
得到曲線![]() ,試判斷點
,試判斷點![]() 的軌跡與曲線
的軌跡與曲線![]() 是否有交點,如果有,請求出交點的直角坐標(biāo),沒有則說明理由.
是否有交點,如果有,請求出交點的直角坐標(biāo),沒有則說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
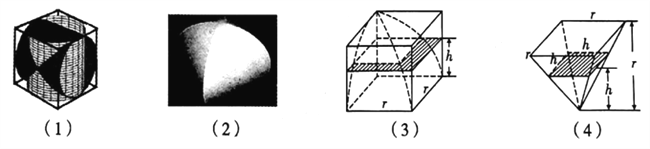
【題目】中國古代數(shù)學(xué)家劉徽在《九章算術(shù)注》中,稱一個正方體內(nèi)兩個互相垂直的內(nèi)切圓柱所圍成的立體為“牟合方蓋”,如圖(1)(2),劉徽未能求得牟合方蓋的體積,直言“欲陋形措意,懼失正理”,不得不說“敢不闕疑,以俟能言者”.約200年后,祖沖之的兒子祖暅提出“冪勢既同,則積不容異”,后世稱為祖暅原理,即:兩等高立體,若在每一等高處的截面積都相等,則兩立體體積相等.如圖(3)(4),祖暅利用八分之一正方體去掉八分之一牟合方蓋后的幾何體與長寬高皆為八分之一正方體的邊長的倒四棱錐“等冪等積”,計算出牟合方蓋的體積,據(jù)此可知,牟合方蓋的體積與其外切正方體的體積之比為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com