
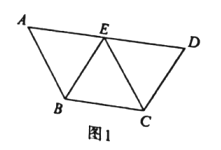
【題目】如圖1,在等腰梯形ABCD中,![]() ,
,![]() ,
,![]() ,E為AD的中點.現分別沿BE,EC將△ABE 和△ECD折起,使得平面ABE⊥平面BCE,平面ECD⊥平面BCE,連接AD,如圖2.
,E為AD的中點.現分別沿BE,EC將△ABE 和△ECD折起,使得平面ABE⊥平面BCE,平面ECD⊥平面BCE,連接AD,如圖2.
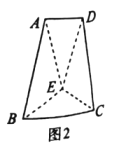
(1)若在平面BCE內存在點G,使得GD∥平面ABE,請問點G的軌跡是什么圖形?并說明理由.
(2)求平面AED與平面BCE所成銳二面角的余弦值.
【答案】(1)點G的軌跡是直線MN,見解析;(2)![]()
【解析】
(1)分別取![]() 和
和![]() 的中點
的中點![]() 和
和![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,根據線線平行可證明平面
,根據線線平行可證明平面![]() 平面
平面![]() ,則可判斷點
,則可判斷點![]() 的軌跡;(2)以點
的軌跡;(2)以點![]() 為坐標原點,
為坐標原點,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 軸,
軸,![]() 所在直線為
所在直線為![]() 軸,建立空間直角坐標系,分別求兩個平面的法向量
軸,建立空間直角坐標系,分別求兩個平面的法向量![]() ,代入公式
,代入公式![]() 求解.
求解.
(1)點G的軌跡是直線MN.
理由:如圖,分別取BC和CE的中點N和M,連接DM,MN,ND,則MN//BE.
又MN![]() 平面BEA,BE
平面BEA,BE![]() 平面BEA,所以MN//平面BEA.
平面BEA,所以MN//平面BEA.
依題意有△ABE,△BCE,△ECD均為邊長為2的正三角形,所以MD⊥CE.
又平面ECD⊥平面BCE,則MD⊥平面BCE.又平面ABE⊥平面BCE,所以MD//平面BEA.
所以平面NMD//平面BEA,則點G的軌跡是直線MN.
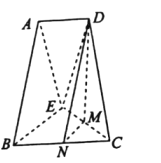
(2)如圖,以點M為坐標原點,MB所在直線為x軸,MC所在直線為y軸,MD所在直線為z軸,建立空間直角坐標系,則E(0,-1,0),D(0,0,![]() ),A
),A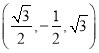 ,所以
,所以 ,
,![]() .
.
設平面AED的法向量為![]() ,則
,則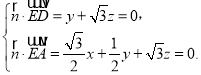
取![]() ,得
,得![]() . 取平面BCE的一個法向量為
. 取平面BCE的一個法向量為![]() ,
,
則![]() , 所以平面AED與平面BCE所成銳二面角的余弦值為
, 所以平面AED與平面BCE所成銳二面角的余弦值為![]() .
.


科目:高中數學 來源: 題型:
【題目】設![]() ,
,![]() 是兩個平面,
是兩個平面,![]() ,
,![]() 是兩條直線,下列命題錯誤的是( )
是兩條直線,下列命題錯誤的是( )
A.如果![]() ,
,![]() ,那么
,那么![]() .
.
B.如果![]() ,
,![]() ,那么
,那么![]() .
.
C.如果![]() ,
,![]() ,
,![]() ,那么
,那么![]() .
.
D.如果![]() 內有兩條相交直線與
內有兩條相交直線與![]() 平行,那么
平行,那么![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]()
![]() 常數
常數![]() )滿足
)滿足![]() .
.
(1)求出![]() 的值,并就常數
的值,并就常數![]() 的不同取值討論函數
的不同取值討論函數![]() 奇偶性;
奇偶性;
(2)若![]() 在區間
在區間![]() 上單調遞減,求
上單調遞減,求![]() 的最小值;
的最小值;
(3)在(2)的條件下,當![]() 取最小值時,證明:
取最小值時,證明:![]() 恰有一個零點
恰有一個零點![]() 且存在遞增的正整數數列
且存在遞增的正整數數列![]() ,使得
,使得![]() 成立.
成立.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 各項均為正數,
各項均為正數,![]() 為其前
為其前![]() 項的和,且
項的和,且![]() 成等差數列.
成等差數列.
(1)寫出![]() 、
、![]() 、
、![]() 的值,并猜想數列
的值,并猜想數列![]() 的通項公式
的通項公式![]() ;
;
(2)證明(1)中的猜想;
(3)設![]() ,
,![]() 為數列
為數列![]() 的前
的前![]() 項和.若對于任意
項和.若對于任意![]() ,都有
,都有![]() ,求實數
,求實數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
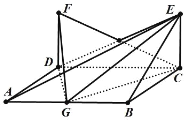
【題目】如圖,在四棱錐 E ABCD 中, EC 底面 ABCD , FD / /EC ,底面 ABCD 為矩形, G 為線段 AB 的中點, CG DG,CD DF CE 2 ,則四棱錐 E ABCD與三棱錐 F CDG 的公共部分的體積為________________ .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司租賃甲、乙兩種設備生產A,B兩類產品,甲種設備每天能生產A類產品5件和B類產品10件,乙種設備每天能生產A類產品6件和B類產品20件.已知設備甲每天的租賃費為200元,設備乙每天的租賃費為300元,現該公司至少要生產A類產品50件,B類產品140件,所需租賃費最少為__________元.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=ex+e-x,其中e是自然對數的底數.
(1)證明:f(x)是R上的偶函數;
(2)若關于x的不等式mf(x)≤e-x+m-1在(0,+∞)上恒成立,求實數m的取值范圍;
(3)已知正數a滿足:存在x0∈[1,+∞),使得f(x0)<a(-![]() +3x0)成立.試比較ea-1與ae-1的大小,并證明你的結論.
+3x0)成立.試比較ea-1與ae-1的大小,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法正確的是( )
A.在頻率分布直方圖中,眾數左邊和右邊的直方圖的面積相等;
B.為調查高三年級的240名學生完成作業所需的時間,由教務處對高三年級的學生進行編號,從001到240抽取學號最后一位為3的學生進行調查,則這種抽樣方法為分層抽樣;
C.“![]() ”是“
”是“![]() ”的必要不充分條件;
”的必要不充分條件;
D.命題![]() :“
:“![]() ,使得
,使得![]() ”的否定為:“
”的否定為:“![]() ,均有
,均有![]() ”.
”.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com