
【題目】已知點A(﹣1,0),B(1,0),C(0,1),直線y=ax+b(a>0)將△ABC分割為面積相等的兩部分,則b的取值范圍是( )
A.(0,1)B. C.
C. D.
D.![]()
【答案】B
【解析】
先求得直線y=ax+b(a>0)與x軸的交點為M(![]() ,0),由
,0),由![]() 0可得點M在射線OA上.求出直線和BC的交點N的坐標,①若點M和點A重合,求得b
0可得點M在射線OA上.求出直線和BC的交點N的坐標,①若點M和點A重合,求得b![]() ;②若點M在點O和點A之間,求得
;②若點M在點O和點A之間,求得![]() b
b![]() ; ③若點M在點A的左側,求得
; ③若點M在點A的左側,求得![]() b>1
b>1![]() .再把以上得到的三個b的范圍取并集,可得結果.
.再把以上得到的三個b的范圍取并集,可得結果.
由題意可得,三角形ABC的面積為 ![]() 1,
1,
由于直線y=ax+b(a>0)與x軸的交點為M(![]() ,0),
,0),
由直線y=ax+b(a>0)將△ABC分割為面積相等的兩部分,可得b>0,
故![]() 0,故點M在射線OA上.
0,故點M在射線OA上.
設直線y=ax+b和BC的交點為N,則由![]() 可得點N的坐標為(
可得點N的坐標為(![]() ,
,![]() ).
).
①若點M和點A重合,如圖:

則點N為線段BC的中點,故N(![]() ,
,![]() ),
),
把A、N兩點的坐標代入直線y=ax+b,求得a=b![]() .
.
②若點M在點O和點A之間,如圖:
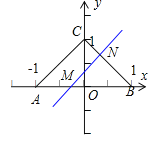
此時b![]() ,點N在點B和點C之間,
,點N在點B和點C之間,
由題意可得三角形NMB的面積等于![]() ,
,
即![]() ,即
,即 ![]() ,可得a
,可得a![]() 0,求得 b
0,求得 b![]() ,
,
故有![]() b
b![]() .
.
③若點M在點A的左側,
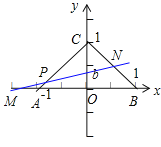
則b![]() ,由點M的橫坐標
,由點M的橫坐標![]() 1,求得b>a.
1,求得b>a.
設直線y=ax+b和AC的交點為P,則由 ![]() 求得點P的坐標為(
求得點P的坐標為(![]() ,
,![]() ),
),
此時,由題意可得,三角形CPN的面積等于![]() ,即
,即 ![]() (1﹣b)|xN﹣xP|
(1﹣b)|xN﹣xP|![]() ,
,
即![]() (1﹣b)|
(1﹣b)|![]() |
|![]() ,化簡可得2(1﹣b)2=|a2﹣1|.
,化簡可得2(1﹣b)2=|a2﹣1|.
由于此時 b>a>0,0<a<1,∴2(1﹣b)2=|a2﹣1|=1﹣a2 .
兩邊開方可得 ![]() (1﹣b)
(1﹣b)![]() 1,∴1﹣b
1,∴1﹣b![]() ,化簡可得 b>1
,化簡可得 b>1![]() ,
,
故有1![]() b
b![]() .
.
綜上可得b的取值范圍應是 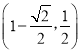 ,
,
故選:B.


科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦距為
的焦距為![]() ,且過點
,且過點![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設![]() 為橢圓
為橢圓![]() 上一點,過點
上一點,過點![]() 作
作![]() 軸的垂線,垂足為
軸的垂線,垂足為![]() .取點
.取點![]() ,連接
,連接![]() ,過點
,過點![]() 作
作![]() 的垂線交
的垂線交![]() 軸于點
軸于點![]() .點
.點![]() 是點
是點![]() 關于
關于![]() 軸的對稱點,作直線
軸的對稱點,作直線![]() ,問這樣作出的直線
,問這樣作出的直線![]() 是否與橢圓
是否與橢圓![]() 一定有唯一的公共點?并說明理由.
一定有唯一的公共點?并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校高二年級共有800名學生參加2019年全國高中數學聯賽江蘇賽區初賽,為了解學生成績,現隨機抽取40名學生的成績(單位:分),并列成如下表所示的頻數分布表:
分組 |
|
|
|
|
|
頻數 |
|
|
|
|
|
⑴試估計該年級成績不低于90分的學生人數;
⑵成績在![]() 的5名學生中有3名男生,2名女生,現從中選出2名學生參加訪談,求恰好選中一名男生一名女生的概率.
的5名學生中有3名男生,2名女生,現從中選出2名學生參加訪談,求恰好選中一名男生一名女生的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】北京101中學校園內有一個“少年湖”,湖的兩側有一個音樂教室和一個圖書館,如圖,若設音樂教室在A處,圖書館在B處,為測量A,B兩地之間的距離,某同學選定了與A,B不共線的C處,構成△ABC,以下是測量的數據的不同方案:①測量∠A,AC,BC;②測量∠A,∠B,BC;③測量∠C,AC,BC;④測量∠A,∠C,∠B. 其中一定能唯一確定A,B兩地之間的距離的所有方案的序號是_______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨著生活水平的提高,越來越多的人參與了潛水這項活動.某潛水中心調查了100名男性與100女性下潛至距離水面5米時是否耳鳴,下圖為其等高條形圖:

①繪出![]() 列聯表;
列聯表;
②根據列聯表的獨立性檢驗,能否在犯錯誤的概率不超過0.005的前提下認為耳鳴與性別有關系?
附:![]() ,其中
,其中![]() .
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com