Question

【題目】某公司為了解用戶對其產品的滿意度，從A，B兩地區分別隨機調查了40個用戶，根據用戶對產品的滿意度評分，得到A地區用戶滿意度評分的頻率分布直方圖和B地區用戶滿意度評分的頻數分布表。

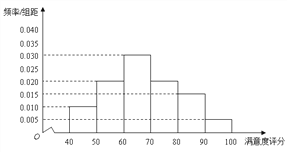
A地區用戶滿意度評分的頻率分布直方圖

B地區用戶滿意度評分的頻數分布表

（Ⅰ）在答題卡上作出B地區用戶滿意度評分的頻率分布直方圖，并通過直方圖比較兩地區滿意度評分的平均值及分散程度（不要求計算出具體值，給出結論即可）；

（Ⅱ）根據用戶滿意度評分，將用戶的滿意度從低到高分為三個等級：

滿意度評分	低于70分	70分到89分	不低于90分
滿意度等級	不滿意	滿意	非常滿意

估計哪個地區的滿意度等級為不滿意的概率大？說明理由

Answer 1

【答案】(1) B地區用戶滿意度評分的平均值高于A地區用戶滿意度評分的平均值；B地區用戶滿意度評分比較集中，而A地區用戶滿意度評分比較分散。(2) A地區用戶的滿意度等級為不滿意的概率大

【解析】試題分析：（I）根據分布表的數據，畫出頻率直方圖，圖形集中的分散程度小，矩形高的多，平均值高。（II）計算得出CA表示事件：“A地區用戶的滿意度等級為不滿意”，CB表示事件：“B地區用戶的滿意度等級為不滿意”，P（CA），P（CB），即可判斷不滿意的情況

解析：

（Ⅰ）

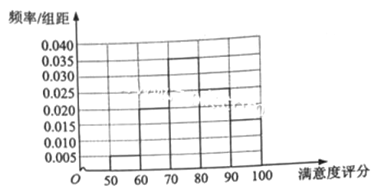
通過兩地區用戶滿意度評分的頻率分布直方圖可以看出，B地區用戶滿意度評分的平均值高于A地區用戶滿意度評分的平均值；B地區用戶滿意度評分比較集中，而A地區用戶滿意度評分比較分散。

（Ⅱ）A地區用戶的滿意度等級為不滿意的概率大。

記表示事件：“A地區用戶的滿意度等級為不滿意”； 記表示事件：“B地區用戶的滿意度等級為不滿意”。

由直方圖得的估計值為

的估計值為

所以A地區用戶的滿意度等級為不滿意的概率大。