【題目】設
，命題p：函數
在
內單調遞增；q：函數
僅在
處有極值.
（1）若命題q是真命題，求a的取值范圍；
（2）若命題
是真命題，求a的取值范圍.
【答案】（1）
；（2）
.
【解析】
(1)函數
僅在
處有極值，則
在左右兩側導數符號相反，可得
恒成立，轉化為求解二次不等式的恒成立問題；（2）當p是真命題時，利用復合函數“同增異減”研究
的單調性問題，求出相應a的范圍，又
是真命題，則
至少有一個是真命題，所以取p是真命題時a的取值集合與
是真命題時a的取值集合的并集即可.
（1）由題意知，，顯然不是方程
的根,
為使僅在處有極值，必須恒成立，即
，
解不等式，得
，這時
是唯一極值，
因此滿足條件的a的取值范圍是
.
（2）當p是真命題時，
對
恒成立,則
，記
，則
當
時，要使得是增函數，則需有
對恒成立，所以
，與矛盾；
當
時，要使得是增函數，則需有
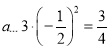對恒成立，所以
，所以
.
記當p是真命題時a的取值集合為A，則
；
記當是真命題時a的取值集合為B，則
.
因為是真命題，
所以a的取值范圍是
.
狀元坊全程突破導練測系列答案科目：高中數學 來源： 題型：
【題目】某高校在2016年的自主招生考試成績中隨機抽取100名學生的筆試成績，按成績分組，得到的頻率分布表如下表所示．
組號 | 分組 | 頻數 | 頻率 |
第1組 |
| 5 | 0.050 |
第2組 |
| n | 0.350 |
第3組 |
| 30 | p |
第4組 |
| 20 | 0.200 |
第5組 |
| 10 | 0.100 |
合計 | 100 | 1.000 |
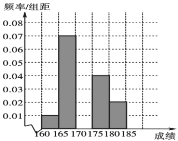
（1）求頻率分布表中n，p
（2）為了能選拔出最優秀的學生，高校決定在筆試成績高的第3、4、5組中用分層抽樣的方法抽取6名學生進入第二輪面試，則第3、4、5組每組各抽取多少名學生進入第二輪面試？
（3）在（2）的前提下，學校決定從6名學生中隨機抽取2名學生接受甲考官的面試，求第4組至少有1名學生被甲考官面試的概率．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
的前
項和為
，
且滿足:
(1)證明：是等比數列，并求數列的通項公式.
(2)設
，若數列
是等差數列，求實數
的值；
(3)在(2)的條件下，設
記數列
的前項和為
，若對任意的
存在實數
,使得
,求實數的最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某市旅游局為了進一步開發旅游資源，需要了解游客的情況，以便制定相應的策略，在某月中隨機抽取甲、乙兩個景點各10天的游客數，畫出莖葉圖如下：若景點甲中的數據的中位數是126，景點乙中的數據的平均數是124.
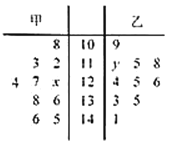
（1）求
，
的值；
（2）若將圖中景點甲中的數據作為該景點較長一段時期內的樣本數據（視樣本頻率為概率）.今從這段時期內任取4天，記其中游客數不低于125人的天數為
，求概率
；
（3）現從上圖的共20天的數據中任取2天的數據（甲、乙兩景點中各取1天），記其中游客數不低于115且不高于135人的天數為
，求的分布列和期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】中國古代數學名著《九章算術》中有這樣一個問題:今有牛、馬、羊食人苗，苗主責之粟五斗，羊主曰:“我羊食半馬、“馬主曰:“我馬食半牛，”今欲衰償之，問各出幾何?此問題的譯文是:今有牛、馬、羊吃了別人的禾苗，禾苗主人要求賠償5斗粟、羊主人說:“我羊所吃的禾苗只有馬的一半，”馬主人說:“我馬所吃的禾苗只有牛的一半，“打算按此比例償還，他們各應償還多少？該問題中，1斗為10升，則馬主人應償還( )升粟？
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某IT從業者繪制了他在26歲～35歲(2009年～2018年)之間各年的月平均收入（單位：千元）的散點圖：
（1）由散點圖知，可用回歸模型
擬合
與
的關系，試根據附注提供的有關數據建立關于的回歸方程
（2）若把月收入不低于2萬元稱為“高收入者”.
試利用（1）的結果，估計他36歲時能否稱為“高收入者”？能否有95%的把握認為年齡與收入有關系？
附注：①.參考數據：
，
，
,
，
，
,
，其中
，取
，
②.參考公式：回歸方程
中斜率
和截距
的最小二乘估計分別為:
，
P（K2≥k） | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
③.
．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
