【題目】△ABC的內角A，B，C的對邊分別為a，b，c，已知2cosC（acosB+bcosA）=c．
（Ⅰ）求C；（Ⅱ）若c=
，△ABC的面積為
，求△ABC的周長．
【答案】(1) C=
(2) △ABC的周長為
+ 
【解析】試題分析：（1）由正弦定理，兩角和的正弦函數公式，三角形內角和定理化簡已知可得2cosCsinC=sinC，結合范圍C∈（0，π），解得cosC=
，可得C的值．（2）由三角形的面積公式可求ab=3，利用余弦定理解得a+b的值，即可得解△ABC的周長．
解析：
（Ⅰ）∵在△ABC中，0＜C＜π，∴sinC≠0
利用正弦定理化簡得：2cosC（sinAcosB+sinBcosA）=sinC，
整理得：2cosCsin（A+B）=sinC，
即2cosCsin（π﹣（A+B））=sinC,2cosCsinC=sinC
∴cosC=
，∴C=
（Ⅱ）由余弦定理得3=a2+b2﹣2ab
，
∴（a+b）2﹣3ab=3，
∵S= 
absinC= 
ab=
， ∴ab=16，
∴（a+b）2﹣48=3，∴a+b=
，
∴△ABC的周長為
+ 
.
舉一反三同步巧講精練系列答案
口算與應用題卡系列答案科目：高中數學 來源： 題型：
【題目】隨著經濟的發展，某城市的市民收入逐年增長，表1是該城市某銀行連續五年的儲蓄存款額(年底余額)：
表1
年份x | 2011 | 2012 | 2013 | 2014 | 2015 |
儲蓄存款額y(千億元) | 5 | 6 | 7 | 8 | 10 |
為了研究計算的方便，工作人員將表1的數據進行了處理，令t＝x－2 010，z＝y－5，得到表2：
表2
時間代號t | 1 | 2 | 3 | 4 | 5 |
z | 0 | 1 | 2 | 3 | 5 |
(1)z關于t的線性回歸方程是________；y關于x的線性回歸方程是________；
(2)用所求回歸方程預測到2020年年底，該銀行儲蓄存款額可達________千億元．
(附：線性回歸方程
＝
x＋
，其中＝
，＝
－
)
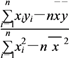查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本小題滿分12分）己知函數f（x）= 
（1）求曲線y=f（x）在點（0，f（0））處的切線方程；
（2）求證：當x∈（0，1）時，f（x）>2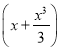
（3）設實數k使得f（x）>k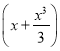
對x∈（0，1）恒成立，求k的最大值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在直角坐標系
中，以坐標原點
為極點， 
軸的正半軸為極軸，建立極坐標系，已知直線
的參數方程為
(
為參數)，曲線
的極坐標方程是
.
(1)寫出直線
的普通方程和曲線
的直角坐標方程；
(2)設直線
與曲線
相交于
兩點，點
為
的中點，點
的極坐標為
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的上、下、左、右四個頂點分別為
x軸正半軸上的某點
滿足
.
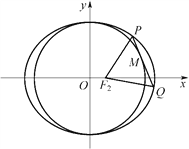
(1)求橢圓的方程;
(2)設該橢圓的左、右焦點分別為
,點
在圓
上,且
在第一象限,過
作圓
的切線交橢圓于
,求證:△
的周長是定值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖1 ,在△ABC中，AB=BC=2, ∠B=90°,D為BC邊上一點，以邊AC為對角線做平行四邊形ADCE，沿AC將△ACE折起，使得平面ACE ⊥平面ABC,如圖2.
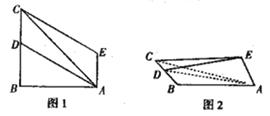
(1)在圖 2中，設M為AC的中點，求證:BM丄AE；
(2)在圖2中，當DE最小時，求二面角A -DE-C的平面角.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】園林管理處擬在公園某區域規劃建設一半徑為
米圓心角為
（弧度）的扇形景觀水池，其中
為扇形
的圓心，同時緊貼水池周邊建一圈理想的無寬度步道，要求總預算費用不超過
萬元，水池造價為每平方米
元，步道造價為每米
元.
（1）當
和
分別為多少時，可使廣場面積最大，并求出最大值；
（2）若要求步道長為
米，則可設計出水池最大面積是多少.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】(2017·合肥市質檢)已知點F為橢圓E： 
(a>b>0)的左焦點，且兩焦點與短軸的一個頂點構成一個等邊三角形，直線
與橢圓E有且僅有一個交點M.
(1)求橢圓E的方程；
(2)設直線
與y軸交于P，過點P的直線l與橢圓E交于不同的兩點A，B，若λ|PM|2＝|PA|·|PB|，求實數λ的取值范圍．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
