
【題目】在平面直角坐標系xOy中,曲線C1的參數方程為![]() (
(![]() 為參數),曲線C2的參數方程為
為參數),曲線C2的參數方程為![]() (
(![]() 為參數).在以O為極點,x軸的正半軸為極軸的極坐標系中,射線l:θ=α 與C1,C2 各有一個交點.當 α=0時,這兩個交點間的距離為2,當 α=
為參數).在以O為極點,x軸的正半軸為極軸的極坐標系中,射線l:θ=α 與C1,C2 各有一個交點.當 α=0時,這兩個交點間的距離為2,當 α=![]() 時,這兩個交點重合.
時,這兩個交點重合.
(1) 求曲線C1,C2的直角坐標方程
(2) 設當 α=![]() 時,l與C1,C2的交點分別為A1,B1,當 α=-
時,l與C1,C2的交點分別為A1,B1,當 α=-![]() 時,l與C1,C2的交點分別為A2,B2,求四邊形A1A2B2B1的面積.
時,l與C1,C2的交點分別為A2,B2,求四邊形A1A2B2B1的面積.
【答案】(1)C1,C2的普通方程分別為x2+y2=1和![]() +y2=1,(2)
+y2=1,(2)![]()
【解析】
(1)令α=0和α=![]() 得a,b 值由參數方程與普通方程的互化求解得C1,C2的普通方程;(2)令α=
得a,b 值由參數方程與普通方程的互化求解得C1,C2的普通方程;(2)令α=![]() ,得A1,B1的橫坐標,利用對稱性得A1,B1關于x軸對稱,得四邊形A1A2B2B1為等腰梯形,利用面積公式求解即可
,得A1,B1的橫坐標,利用對稱性得A1,B1關于x軸對稱,得四邊形A1A2B2B1為等腰梯形,利用面積公式求解即可
由題C1 的普通方程為x2+y2=1;C2的普通方程為![]()
當α=0時,射線l與C1,C2交點的直角坐標分別為(1,0),(a,0),因為這兩點間的距離為2,所以a=3.
當α=![]() 時,射線l與C1,C2交點的直角坐標分別為(0,1),(0,b),因為這兩點重合,所以b=1.
時,射線l與C1,C2交點的直角坐標分別為(0,1),(0,b),因為這兩點重合,所以b=1.
故C1,C2的普通方程分別為x2+y2=1和![]() +y2=1,
+y2=1,
(2)當α=![]() 時,射線l與C1交點A1的橫坐標為x=
時,射線l與C1交點A1的橫坐標為x=![]() ,與C2交點B1的橫坐標為x′=
,與C2交點B1的橫坐標為x′=![]() .
.
當α=-![]() 時,射線l與C1,C2的兩個交點A2,B2分別與A1,B1關于x軸對稱,因此四邊形A1A2B2B1為梯形.
時,射線l與C1,C2的兩個交點A2,B2分別與A1,B1關于x軸對稱,因此四邊形A1A2B2B1為梯形.
故四邊形A1A2B2B1的面積為![]() .
.


科目:高中數學 來源: 題型:
【題目】某地區發現某污染源,相關部門對污染情況進行調查研究后,發現一天中污染指數![]() 與時刻x(時)的函數關系為
與時刻x(時)的函數關系為![]() ,其中a是與氣象有關的參數,且
,其中a是與氣象有關的參數,且![]() .按規定,若每天污染指數不超過2,則環保合格,否則需要整改.如果以每天中
.按規定,若每天污染指數不超過2,則環保合格,否則需要整改.如果以每天中![]() 的最大值作為當天的污染指數,并記為
的最大值作為當天的污染指數,并記為![]() ,那么該地區污染指數的超標情況為________.
,那么該地區污染指數的超標情況為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于函數圖象的有下列說法:
①若函數![]() 滿足
滿足![]() ,則
,則![]() 的一個周期為
的一個周期為![]() ;
;
②若函數![]() 滿足
滿足![]() ,則
,則![]() 的圖象關于直線
的圖象關于直線![]() 對稱;
對稱;
③函數![]() 與函數
與函數![]() 的圖象關于直線
的圖象關于直線![]() 對稱;
對稱;
④若函數![]() 與函數
與函數![]() 的圖象關于原點對稱,則
的圖象關于原點對稱,則![]() ,
,
其中正確的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某醫藥開發公司實驗室有![]() 瓶溶液,其中
瓶溶液,其中![]() 瓶中有細菌
瓶中有細菌![]() ,現需要把含有細菌
,現需要把含有細菌![]() 的溶液檢驗出來,有如下兩種方案:
的溶液檢驗出來,有如下兩種方案:
方案一:逐瓶檢驗,則需檢驗![]() 次;
次;
方案二:混合檢驗,將![]() 瓶溶液分別取樣,混合在一起檢驗,若檢驗結果不含有細菌
瓶溶液分別取樣,混合在一起檢驗,若檢驗結果不含有細菌![]() ,則
,則![]() 瓶溶液全部不含有細菌
瓶溶液全部不含有細菌![]() ;若檢驗結果含有細菌
;若檢驗結果含有細菌![]() ,就要對這
,就要對這![]() 瓶溶液再逐瓶檢驗,此時檢驗次數總共為
瓶溶液再逐瓶檢驗,此時檢驗次數總共為![]() .
.
(1)假設![]() ,采用方案一,求恰好檢驗3次就能確定哪兩瓶溶液含有細菌
,采用方案一,求恰好檢驗3次就能確定哪兩瓶溶液含有細菌![]() 的概率;
的概率;
(2)現對![]() 瓶溶液進行檢驗,已知每瓶溶液含有細菌
瓶溶液進行檢驗,已知每瓶溶液含有細菌![]() 的概率均為
的概率均為![]() .
.
若采用方案一.需檢驗的總次數為![]() ,若采用方案二.需檢驗的總次數為
,若采用方案二.需檢驗的總次數為![]() .
.
(i)若![]() 與
與![]() 的期望相等.試求
的期望相等.試求![]() 關于
關于![]() 的函數解析式
的函數解析式![]() ;
;
(ii)若![]() ,且采用方案二總次數的期望小于采用方案一總次數的期望.求
,且采用方案二總次數的期望小于采用方案一總次數的期望.求![]() 的最大值.
的最大值.
參考數據:![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地舉辦水果觀光采摘節,并推出配套旅游項目,統計了4月份100名游客購買水果的情況,得到如圖所示的頻率分布直方圖.
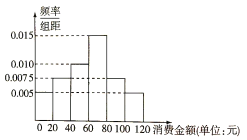
(1)若將消費金額不低于80元的游客稱為“水果達人”,現用分層抽樣的方法從樣本的“水果達人”中抽取5人,求這5人中消費金額不低于100元的人數;
(2)從(1)中的5人中抽取2人作為幸運客戶免費參加配套旅游項目,請列出所有的可能結果,并求這2人中至少有1人購買金額不低于100元的概率;
(3)為吸引顧客,該地特推出兩種促銷方案,
方案一:每滿80元可立減8元;
方案二:金額超過50元但又不超過80元的部分打9折,金額超過80元但又不超過100元的部分打8折,金額超過100元的部分打7折.
若水果的價格為11元/千克,某游客要購買10千克,應該選擇哪種方案.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查某大學學生在某天上網的時間,隨機對100名男生和100名女生進行了不記名的問卷調查,得到了如下的統計結果:

(1)若該大學共有女生750人,試估計其中上網時間不少于60分鐘的人數;
(2)完成聯表,并回答能否有90%的把握認為“大學生上網時間與性別有關”.

附:![]() ,其中n=a+b+c+d為樣本容量.
,其中n=a+b+c+d為樣本容量.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,過原點
,過原點![]() 且斜率為1的直線
且斜率為1的直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,四邊形
兩點,四邊形![]() 的周長與面積分別為8與
的周長與面積分別為8與![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)設直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,且
兩點,且![]() ,求證:
,求證:![]() 到直線
到直線![]() 的距離為定值.
的距離為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com