
【題目】如圖,在平面直角坐標系![]() 中,橢圓
中,橢圓![]() :
:![]() 的離心率為
的離心率為![]() ,焦點到相應準線的距離為
,焦點到相應準線的距離為![]() ,
,![]() ,
,![]() 分別為橢圓的左頂點和下頂點,
分別為橢圓的左頂點和下頂點,![]() 為橢圓
為橢圓![]() 上位于第一象限內的一點,
上位于第一象限內的一點,![]() 交
交![]() 軸于點
軸于點![]() ,
,![]() 交
交![]() 軸于點
軸于點![]() .
.
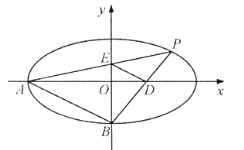
(1)求橢圓![]() 的標準方程;
的標準方程;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)求證:四邊形![]() 的面積為定值.
的面積為定值.
 優學名師名題系列答案
優學名師名題系列答案科目:高中數學 來源: 題型:
【題目】將函數![]() 的圖象向左平移
的圖象向左平移![]() 個單位長度,再向上平移1個單位長度,得到函數g(x)的圖象,則函數g(x)具有性質_____.(填入所有正確結論的序號)
個單位長度,再向上平移1個單位長度,得到函數g(x)的圖象,則函數g(x)具有性質_____.(填入所有正確結論的序號)
①最大值為![]() ,圖象關于直線
,圖象關于直線![]() 對稱;
對稱;
②圖象關于y軸對稱;
③最小正周期為π;
④圖象關于點![]() 對稱.
對稱.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線C的頂點為原點,焦點F與圓![]() 的圓心重合.
的圓心重合.
(1)求拋物線C的標準方程;
(2)設定點![]() ,當P點在C上何處時,
,當P點在C上何處時,![]() 的值最小,并求最小值及點P的坐標;
的值最小,并求最小值及點P的坐標;
(3)若弦![]() 過焦點
過焦點![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】交通管理部門為了解機動車駕駛員(簡稱駕駛員)對某新法規的知曉情況,對甲、乙、丙、丁四個社區做分層抽樣調查.假設四個社區駕駛員的總人數為N,其中甲社區有駕駛員96人.若在甲、乙、丙、丁四個社區抽取駕駛員的人數分別為12,21,25,43,則這四個社區駕駛員的總人數N為( )
A.101
B.808
C.1212
D.2012
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知等比數列![]() 的前
的前![]() 項和為
項和為![]() ,公比
,公比![]() ,
,![]() ,
,![]() .
.
(1)求等比數列![]() 的通項公式;
的通項公式;
(2)設![]() ,求
,求![]() 的前
的前![]() 項和
項和![]() .
.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)將已知兩式作差,利用等比數列的通項公式,可得公比,由等比數列的求和可得首項,進而得到所求通項公式;(2)求得bn=n,![]() ,由裂項相消求和可得答案.
,由裂項相消求和可得答案.
(1)等比數列![]() 的前
的前![]() 項和為
項和為![]() ,公比
,公比![]() ,
,![]() ①,
①,
![]() ②.
②.
②﹣①,得![]() ,則
,則![]() ,
,
又![]() ,所以
,所以![]() ,
,
因為![]() ,所以
,所以![]() ,
,
所以![]() ,
,
所以![]() ;
;
(2)![]() ,
,![]()
所以前![]() 項和
項和![]() .
.
【點睛】
裂項相消法適用于形如 (其中
(其中![]() 是各項均不為零的等差數列,c為常數)的數列. 裂項相消法求和,常見的有相鄰兩項的裂項求和,還有一類隔一項的裂項求和,如
是各項均不為零的等差數列,c為常數)的數列. 裂項相消法求和,常見的有相鄰兩項的裂項求和,還有一類隔一項的裂項求和,如![]() 或
或![]() .
.
【題型】解答題
【結束】
22
【題目】已知函數![]() 的圖象上有兩點
的圖象上有兩點![]() ,
,![]() .函數
.函數![]() 滿足
滿足![]() ,且
,且![]() .
.
(1)求證:![]() ;
;
(2)求證:![]() ;
;
(3)能否保證![]() 和
和![]() 中至少有一個為正數?請證明你的結論.
中至少有一個為正數?請證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列兩個命題:命題p1:a,b∈(0,+∞),當a+b=1時, ![]() +
+ ![]() =4;命題p2:函數y=ln
=4;命題p2:函數y=ln ![]() 是偶函數.則下列命題是真命題的是( )
是偶函數.則下列命題是真命題的是( )
A.p1∧p2
B.p1∧(¬p2)
C.(¬p1)∨p2
D.(¬p1)∨(¬p2)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在正整數數列中,由1開始依次按如下規則,將某些數取出.先取1;再取1后面兩個偶數2,4;再取4后面最鄰近的3個連續奇數5,7,9;再取9后面的最鄰近的4個連續偶數10,12,14,16;再取此后最鄰近的5個連續奇數17,19,21,23,25.按此規則一直取下去,得到一個新數列1,2,4,5,7,9,10,12,14,16,17,…,則在這個新數列中,由1開始的第2 019個數是( )
A. 3 971B. 3 972C. 3 973D. 3 974
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com