
【題目】已知函數![]() (
(![]() ),
),![]() (
(![]() ).
).
(1)討論![]() 的單調性;
的單調性;
(2)設![]() ,
, ![]() ,若
,若![]() (
(![]() )是
)是![]() 的兩個零點,且
的兩個零點,且![]() ,
,
試問曲線![]() 在點
在點![]() 處的切線能否與
處的切線能否與![]() 軸平行?請說明理由.
軸平行?請說明理由.
【答案】(1)當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 單調遞增,
單調遞增, 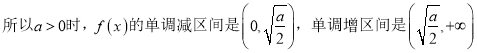 ;(2)
;(2)![]() 在
在![]() 處的切線不能平行于
處的切線不能平行于![]() 軸. 。
軸. 。
【解析】試題分析:(1)先對函數求導,再依據到函數值與函數單調性之間的關系分類探求單調區間;(2)先假設曲線![]() 在點
在點![]() 處的切線能否與
處的切線能否與![]() 軸平行,然后依據假設建立方程組,最后再構造函數
軸平行,然后依據假設建立方程組,最后再構造函數![]() 運用導數的知識斷定假設不成立。
運用導數的知識斷定假設不成立。
解:(Ⅰ) ![]()
(1)當![]() 時,
時, ![]() ,
, ![]() 在
在![]() 單調遞增,
單調遞增,
(2)當![]() 時,
時, ![]() 有
有
|
|
|
|
| - | 0 | + |
| ↘ | 極小值 | ↗ |
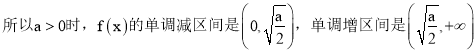
(Ⅱ) ![]()
假設![]() 在
在![]() 處的切線能平行于
處的切線能平行于![]() 軸.
軸.
∵![]()
由假設及題意得:
![]() .................
.................
![]() ................
................
![]() .................
.................
![]() .............④
.............④
由-得, ![]()
即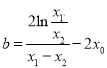 .................⑤
.................⑤
由④⑤得, 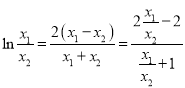
令![]() ,
, ![]() .則上式可化為
.則上式可化為![]() ,
,
設函數![]() ,則
,則
 ,
,
所以函數![]() 在
在![]() 上單調遞增.
上單調遞增.
于是,當![]() 時,有
時,有![]() ,即
,即![]() 與⑥矛盾.
與⑥矛盾.
所以![]() 在
在![]() 處的切線不能平行于
處的切線不能平行于![]() 軸.
軸.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=kx+log9(9x+1)(k∈R)是偶函數.
(1)求k的值;
(2)若函數g(x)=log9(a3x﹣ ![]() a)的圖象與f(x)的圖象有且只有一個公共點,求a的取值范圍.
a)的圖象與f(x)的圖象有且只有一個公共點,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列 ![]() ,﹣
,﹣ ![]() ,
, ![]() ,﹣
,﹣ ![]() ,…的一個通項公式為( )
,…的一個通項公式為( )
A.an=(﹣1)n ![]()
B.an=(﹣1)n ![]()
C.an=(﹣1)n+1 ![]()
D.an=(﹣1)n+1 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在△ABC中,角A,B,C所對的邊分別為a,b,c,且滿足 ![]() acosC﹣csinA=0.
acosC﹣csinA=0.
(1)求角C的大小;
(2)已知b=4,△ABC的面積為6 ![]() ,求邊長c的值.
,求邊長c的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列{an}滿足a1=1,an+1 ![]() =1,記Sn=a12+a22+…+an2 , 若S2n+1﹣Sn≤
=1,記Sn=a12+a22+…+an2 , 若S2n+1﹣Sn≤ ![]() 對任意n∈N*恒成立,則正整數m的最小值是 .
對任意n∈N*恒成立,則正整數m的最小值是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定橢圓C: ![]() (a>b>0).稱圓心在原點O,半徑為
(a>b>0).稱圓心在原點O,半徑為 ![]() 的圓是橢圓C的“準圓”.若橢圓C的一個焦點為F(
的圓是橢圓C的“準圓”.若橢圓C的一個焦點為F( ![]() ,0),其短軸上的一個端點到點F的距離為
,0),其短軸上的一個端點到點F的距離為 ![]() .
.
(1)求橢圓C的方程和其“準圓”方程;
(2)點P是橢圓C的“準圓”上的一個動點,過動點P作直線l1 , l2 , 使得l1 , l2與橢圓C都只有一個交點,試判斷l1 , l2是否垂直,并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com