
【題目】已知過點![]() 的動直線
的動直線![]() 與拋物線
與拋物線![]() :
:![]() 相交于
相交于![]() 兩點.當直線
兩點.當直線![]() 的斜率是
的斜率是![]() 時,
時,![]() .
.
(1)求拋物線![]() 的方程;
的方程;
(2)設線段![]() 的中垂線在
的中垂線在![]() 軸上的截距為
軸上的截距為![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(1)x2=4y;(2)b∈(2,+∞).
【解析】
試題分析:本題主要考查拋物線的標準方程、直線與拋物線的交點問題等基礎知識,考查學生的分析問題解決問題的能力、轉化能力、計算能力.第一問,利用點斜式先寫出直線![]() 的方程,令直線與拋物線聯立,消參得到關于y的方程,利用韋達定理,得到
的方程,令直線與拋物線聯立,消參得到關于y的方程,利用韋達定理,得到![]() 和
和![]() ,再利用
,再利用![]() ,解出
,解出![]() ,得到拋物線的方程;第二問,設出直線
,得到拋物線的方程;第二問,設出直線![]() 的方程,令拋物線與直線聯立,消參得到關于x的方程,利用韋達定理,得到BC的中點坐標,從而得到BC的中垂線方程,令x=0,得到中垂線在y軸上的截距,再通過配方法求范圍.
的方程,令拋物線與直線聯立,消參得到關于x的方程,利用韋達定理,得到BC的中點坐標,從而得到BC的中垂線方程,令x=0,得到中垂線在y軸上的截距,再通過配方法求范圍.
試題解析:(1)設B(x1,y1),C(x2,y2),當直線l的斜率是時,l的方程為y=(x+4),即x=2y-4.
由 得2y2-(8+p)y+8=0,
得2y2-(8+p)y+8=0,
∴![]() ①,
①, ![]() ②
②
又∵![]() ,∴y2=4y1,③
,∴y2=4y1,③
由①②③及p>0得:y1=1,y2=4,p=2,得拋物線G的方程為x2=4y.
(2)設l:y=k(x+4),BC的中點坐標為(x0,y0),
由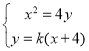 得x2-4kx-16k=0,④
得x2-4kx-16k=0,④
∴![]() ,y0=k(x0+4)=2k2+4k.
,y0=k(x0+4)=2k2+4k.
∴線段BC的中垂線方程為y-2k2-4k=-![]() (x-2k),
(x-2k),
∴線段BC的中垂線在y軸上的截距為:b=2k2+4k+2=2(k+1)2,
對于方程④,由Δ=16k2+64k>0得k>0或k<-4. ∴b∈(2,+∞).


科目:高中數學 來源: 題型:
【題目】某金匠以黃金為原材料加工一種飾品,經多年的數據統計得知,該金匠平均每加5 個飾品中有4個成品和1個廢品,每個成品可獲利3萬元,每個廢品損失1萬元,假設該金匠加工每件飾品互不影響,以頻率估計概率.
(1)若金金匠加工4個飾品,求其中廢品的數量不超過1的概率;
(2)若該金匠加工了 3個飾品,求他所獲利潤的數學期望.
(兩小問的計算結果都用分數表示)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】從某校高三上學期期末數學考試成績中,隨機抽取了![]() 名學生的成績得到如圖所示的頻率分布直方圖:
名學生的成績得到如圖所示的頻率分布直方圖:
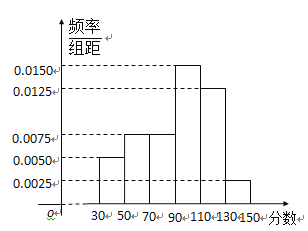
(1)根據頻率分布直方圖,估計該校高三學生本次數學考試的平均分;
(2)若用分層抽樣的方法從分數在![]() 和
和![]() 的學生中共抽取
的學生中共抽取![]() 人,該
人,該![]() 人中成績在
人中成績在![]() 的有幾人?
的有幾人?
(3)在(2)中抽取的![]() 人中,隨機抽取
人中,隨機抽取![]() 人,求分數在
人,求分數在![]() 和
和![]() 各
各![]() 人的概率.
人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() 是
是![]() 上的點.
上的點.
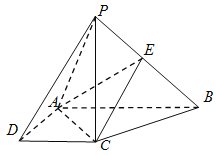
(Ⅰ)求證:平面![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)若![]() 是
是![]() 的中點,且二面角
的中點,且二面角![]() 的余弦值為
的余弦值為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲乙丙丁四個物體同時從某一點出發向同一個方向運動,其路程fi(x)(i=1,2,3,4)關于時間x(x≥0)的函數關系式分別為 ![]() , 有以下結論:
, 有以下結論:
①當x>1時,甲在最前面;
②當x>1時,乙在最前面;
③當0<x<1時,丁在最前面,當x>1時,丁在最后面;
④丙不可能在最前面,也不可能最最后面;
⑤如果它們已知運動下去,最終在最前面的是甲.
其中,正確結論的序號為(把正確結論的序號都填上,多填或少填均不得分)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com