
【題目】已知數列![]() 和
和![]() 都是等差數列,
都是等差數列,![]() .數列
.數列![]() 滿足
滿足![]() .
.
(1)求![]() 的通項公式;
的通項公式;
(2)證明:![]() 是等比數列;
是等比數列;
(3)是否存在首項為1,公比為q的等比數列![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() 成立?若存在,求出q的取值范圍;若不存在,請說明理由.
成立?若存在,求出q的取值范圍;若不存在,請說明理由.
【答案】(1)![]() ;(2)證明見解析;(3)存在,
;(2)證明見解析;(3)存在,![]() .
.
【解析】
(1)設![]() 的公差為d,可得
的公差為d,可得![]() ,
,![]() , 由
, 由![]() 是等差數列,可得
是等差數列,可得![]() 成等差數列,可得
成等差數列,可得![]() ,求出
,求出![]() 的值,可得
的值,可得![]() 的通項公式;
的通項公式;
(2)將![]() 展開,可得
展開,可得![]() ,將
,將![]() 代入此式子相減,可得
代入此式子相減,可得![]() ,再將
,再將![]() 代入此式子相減,可得
代入此式子相減,可得![]() ,此時
,此時![]() ,驗證
,驗證![]() 時也滿足可得
時也滿足可得![]() 是等比數列;
是等比數列;
(3)設存在![]() 對任意
對任意![]() ,都有
,都有![]() 恒成立,即
恒成立,即![]() ,
,![]() ,易得
,易得![]() ,由由
,由由![]() 得,
得,![]() ,可得設
,可得設![]() ,對其求導,可得其最小值,可得q的取值范圍.
,對其求導,可得其最小值,可得q的取值范圍.
解:(1)因為數列![]() 是等差數列,設
是等差數列,設![]() 的公差為d,則
的公差為d,則
![]() ,
,![]() ,
,
因為![]() 是等差數列,所以
是等差數列,所以![]() 成等差數列,
成等差數列,
即![]() ,
,![]() ,
,
解得![]() ,當
,當![]() 時,
時,![]() ,此時
,此時![]() 是等差數列.
是等差數列.
故![]() .
.
(2)由![]() ,即
,即![]() , ①
, ①
所以![]() , ②
, ②
②-①得,![]() , ③
, ③
所以,![]() , ④
, ④
④-③得,![]() ,即
,即![]() 時,
時,![]() ,
,
在①中分別令![]() 得,
得,![]() ,也適合上式,
,也適合上式,
所以![]() ,
,![]() ,
,
因為![]() 是常數,所以
是常數,所以![]() 是等比數列.
是等比數列.
(3)設存在![]() 對任意
對任意![]() ,都有
,都有![]() 恒成立,
恒成立,
即![]() ,
,![]() ,
,
顯然![]() ,由
,由![]() 可知,
可知,![]() ,
,
由![]() 得,
得,![]() ,
,![]() .
.
設![]() ,因為
,因為![]() ,
,
所以當![]() 時,
時,![]() ,
,![]() 遞增;
遞增;
當![]() 時,
時,![]() ,
,![]() 遞減.
遞減.
因為![]() ,所以
,所以![]() ,
,
解得![]() ,
,
綜上可得,存在等比數列![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() 恒成立, 其中公比
恒成立, 其中公比![]() 的取值范圍是
的取值范圍是![]() .
.


 本土教輔贏在暑假高效假期總復習云南科技出版社系列答案
本土教輔贏在暑假高效假期總復習云南科技出版社系列答案 暑假作業北京藝術與科學電子出版社系列答案
暑假作業北京藝術與科學電子出版社系列答案 第三學期贏在暑假系列答案
第三學期贏在暑假系列答案科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為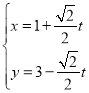 (
(![]() 為參數且
為參數且![]() ).在以坐標原點為極點,
).在以坐標原點為極點,![]() 軸的正半軸為極軸的極坐標系中,曲線
軸的正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的極坐標方程及曲線
的極坐標方程及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 在直線
在直線![]() 上,點
上,點![]() 在曲線
在曲線![]() 上,求證:
上,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓![]() (
(![]() )的離心率是
)的離心率是![]() ,點
,點![]() 在短軸
在短軸![]() 上,且
上,且![]() 。
。
(1)球橢圓![]() 的方程;
的方程;
(2)設![]() 為坐標原點,過點
為坐標原點,過點![]() 的動直線與橢圓交于
的動直線與橢圓交于![]() 兩點。是否存在常數
兩點。是否存在常數![]() ,使得
,使得![]() 為定值?若存在,求
為定值?若存在,求![]() 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在直四棱柱ABCD-A1B1C1D1中,AD//平面BCC1B1,AD⊥DB.求證:
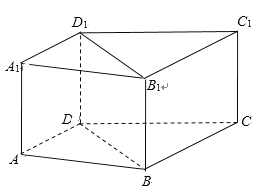
(1)BC//平面ADD1A1;
(2)平面BCC1B1⊥平面BDD1B1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某人某天的工作是:駕車從![]() 地出發,到
地出發,到![]() 兩地辦事,最后返回
兩地辦事,最后返回![]() 地,
地,![]() 三地之間各路段行駛時間及當天降水概率如表:
三地之間各路段行駛時間及當天降水概率如表:
路段 | 正常行駛所需時間(小時) | 上午降水概率 | 下午降水概率 |
| 2 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到降水,則在該路段行駛的時間需延長1小時,現有如下兩個方案:
方案甲:上午從![]() 地出發到
地出發到![]() 地辦事,然后到達
地辦事,然后到達![]() 地,下午在
地,下午在![]() 地辦事后返回
地辦事后返回![]() 地;
地;
方案乙:上午從![]() 地出發到
地出發到![]() 地辦事,下午從
地辦事,下午從![]() 地出發到達
地出發到達![]() 地, 辦事后返回
地, 辦事后返回![]() 地.
地.
(1)設此人8點從![]() 地出發,在各地辦事及午餐的累積時間為2小時.且采用方案甲,求他當日18點或18點之前能返回
地出發,在各地辦事及午餐的累積時間為2小時.且采用方案甲,求他當日18點或18點之前能返回![]() 地的概率;
地的概率;
(2)甲、乙兩個方案中,哪個方案有利于辦完事后能更早返回![]() 地?
地?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國“一帶一路”戰略構思提出后,某科技企業為抓住“一帶一路”帶來的機遇,決定開發生產一款大型電子設備.生產這種設備的年固定成本為500萬元,每生產x臺,需另投入成本![]() 萬元
萬元![]() ,當年產量不足60臺時,
,當年產量不足60臺時,![]() 萬元
萬元![]() ;當年產量不小于60臺時,
;當年產量不小于60臺時,![]() 萬元
萬元![]() 若每臺設備售價為100萬元,通過市場分析,該企業生產的電子設備能全部售完.
若每臺設備售價為100萬元,通過市場分析,該企業生產的電子設備能全部售完.
![]() 求年利潤
求年利潤![]() 萬元
萬元![]() 關于年產量
關于年產量![]() 臺
臺![]() 的函數關系式;
的函數關系式;
![]() 當年產量為多少臺時,該企業在這一電子設備的生產中所獲利潤最大?
當年產量為多少臺時,該企業在這一電子設備的生產中所獲利潤最大?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,橢圓
,橢圓![]() 截直線
截直線![]() 所得的線段的長度為
所得的線段的長度為![]() .
.
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)設直線![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,點
兩點,點![]() 是橢圓
是橢圓![]() 上的點,
上的點,![]() 是坐標原點,若
是坐標原點,若![]() ,判定四邊形
,判定四邊形![]() 的面積是否為定值?若為定值,求出定值;如果不是,請說明理由.
的面積是否為定值?若為定值,求出定值;如果不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,
中,![]() 的參數方程為
的參數方程為 (t為參數).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為
(t為參數).以坐標原點O為極點,x軸的正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]() .
.
(1)求![]() 的普通方程和曲線C的直角坐標方程;
的普通方程和曲線C的直角坐標方程;
(2)求曲線C上的點到![]() 距離的最大值及該點坐標.
距離的最大值及該點坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com