【題目】已知定義在
上的函數
，
為其導數，且
恒成立，則（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
通過
，可以聯想到導數運算的除法，這樣可以構造新函數
，
，這樣就可以判斷出函數
在
上的單調性，把四個選項變形，利用單調性判斷出是否正確.
通過,這個結構形式，可以構造新函數，
，而，所以當時，
，所以函數在上是單調遞增函數，現對四個選項逐一判斷：
選項A. 
,可以判斷
是否正確，
也就是判斷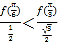
是否正確，即判斷
是否成立，因為
，在上是單調遞增函數，所以有，故選項A正確；
選項B.
，也就是判斷
是否正確，即判斷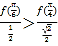
是否成立，即判斷
是否成立，因為
，在上是單調遞增函數，所以有
，故選項B不正確；
選項C. 
，也就是判斷
是否正確，即判斷
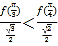是否成立，即判斷
是否成立，因為
，在上是單調遞增函數，所以有
，故選項C不正確；
選項D.
，也就是判斷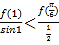
，是否成立，即判斷
是否成立，因為
，在上是單調遞增函數，所以有
，因此選項D不正確，故本題選A.
ABC考王全優卷系列答案科目：高中數學 來源： 題型：
【題目】學生李明用手機加了一個有關高中數學學習的微信群，群里面許多數學愛好者經常發一些有關高中數學學習的心得和經驗，但是，這些心得和經驗的正確性無法保證，下面是李明搜集到的有關函數的一些結論：
（1）若函數
有反函數，則其反函數可表示為
；
（2）函數
在其定義域內的最大值為
，最小值為
，則其值域為
；
（3）定義在
上的函數，若對任意的實數
，
等式
均成立，則函數一定是奇函數；
（4）定義在上的函數，若對任意的實數都有
，則函數一定沒有反函數．
李明的同學們對以上四個結論有以下不同判斷，其中判斷正確的是（ ）
A.都是錯誤的B.只有一個是正確的
C.兩對兩錯D.只有一個是錯誤的
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以下命題：①根據斜二測畫法，三角形的直觀圖是三角形；②有兩個平面互相平行，其余各面都是平行四邊形的多面體是棱柱；③兩相鄰側面所成角相等的棱錐是正棱錐；④若兩個二面角的半平面互相垂直，則這兩個二面角的大小相等或互補.其中正確命題的個數為（ ）
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某縣畜牧技術員張三和李四9年來一直對該縣山羊養殖業的規模進行跟蹤調查，張三提供了該縣某山羊養殖場年養殖數量y(單位：萬只)與相成年份x(序號)的數據表和散點圖(如圖所示)，根據散點圖，發現y與x有較強的線性相關關系，李四提供了該縣山羊養殖場的個數z(單位：個)關于x的回歸方程
.
(1)根據表中的數據和所給統計量，求y關于x的線性回歸方程(參考統計量：
)；
(2)試估計：①該縣第一年養殖山羊多少萬只?
②到第幾年，該縣山羊養殖的數量與第一年相比縮小了?
附：對于一組數據
，其回歸直線
的斜率和截距的最小二乘估計分別為
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】先閱讀下列不等式的證法，再解決后面的問題：
已知
，
，求證：
.
證明：構造函數
，
即
.
因為對一切
，恒有
，
所以
，從而得.
（1）若
，
，請寫出上述結論的推廣式；
（2）參考上述證法，對你推廣的結論加以證明.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】隨著人民生活水平的提高，對城市空氣質量的關注度也逐步增大，圖2是某城市1月至8月的空氣質量檢測情況，圖中一、二、三、四級是空氣質量等級， 一級空氣質量最好，一級和二級都是質量合格天氣，下面四種說法正確的是（ ）
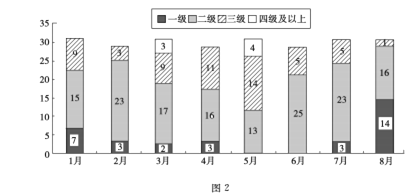
①1月至8月空氣合格天數超過20天的月份有5個
②第二季度與第一季度相比，空氣達標天數的比重下降了
③8月是空氣質量最好的一個月
④6月份的空氣質量最差
A. ①②③ B. ①②④ C. ①③④ D. ②③④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
