
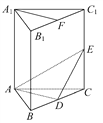
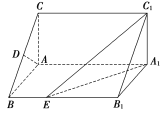
【題目】如圖,在直三棱柱ABC-A1B1C1中,A1B1=A1C1,D,E分別是棱BC,CC1上的點(點D不同于點C),且AD⊥DE,F為B1C1的中點.
求證:(1)平面ADE⊥平面BCC1B1.
(2)直線A1F∥平面ADE.
【答案】(1)見解析;(2)見解析
【解析】試題分析:(1)由三棱柱得CC1⊥平面ABC,因此CC1⊥AD,進而可得AD⊥平面BCC1B1,根據面面垂直的判定定理可得平面ADE⊥平面BCC1B1.(2)由題意得A1F⊥B1C1,又由CC1⊥平面A1B1C1,得CC1⊥A1F,所以A1F⊥平面BCC1B1,又,AD⊥平面BCC1B1, 所以A1F∥AD,根據線面平行的判定定理可得直線A1F∥平面ADE.
試題解析:
(1)因為三棱柱ABC-A1B1C1是直三棱柱,
所以CC1⊥平面ABC,
又因為AD平面ABC,
所以CC1⊥AD.
因為AD⊥DE,CC1,DE平面BCC1B1,且CC1∩DE=E,
所以AD⊥平面BCC1B1,
又因為AD平面ADE,
所以平面ADE⊥平面BCC1B1.
(2)因為A1B1=A1C1,F為B1C1的中點,
所以A1F⊥B1C1,
又CC1⊥平面A1B1C1,且A1F平面A1B1C1,
所以CC1⊥A1F,
又因為CC1,B1C1平面BCC1B1,且CC1∩B1C1=C1,
所以A1F⊥平面BCC1B1,
由(1)知,AD⊥平面BCC1B1,
所以A1F∥AD,
又因為AD平面ADE,A1F平面ADE,
所以直線A1F∥平面ADE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】國際奧委會將于2017年9月15日在秘魯利馬召開130次會議決定2024年第33屆奧運
會舉辦地。目前德國漢堡、美國波士頓等申辦城市因市民擔心賽事費用超支而相繼退出。某機構為調查我國公民對申辦奧運會的態度,選了某小區的100位居民調查結果統計如下:
支持 | 不支持 | 合計 | |
年齡不大于50歲 | 80 | ||
年齡大于50歲 | 10 | ||
合計 | 70 | 100 |
(1)根據已有數據,把表格數據填寫完整;
(2)能否在犯錯誤的概率不超過5%的前提下認為不同年齡與支持申辦奧運無關?
(3)已知在被調查的年齡大于50歲的支持者中有5名女性,其中2位是女教師,現從這5名女性中隨機抽取3人,求至多有1位教師的概率.
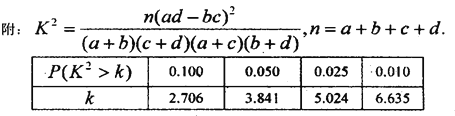
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正四棱錐P-ABCD中,底面邊長為2,側棱長為![]() ,M,N分別為AB,BC的中點,以O為原點,射線OM,ON,OP分別為x軸、y軸、z軸的正方向建立空間直角坐標系.若E,F分別為PA,PB的中點,求A,B,C,D,E,F的坐標.
,M,N分別為AB,BC的中點,以O為原點,射線OM,ON,OP分別為x軸、y軸、z軸的正方向建立空間直角坐標系.若E,F分別為PA,PB的中點,求A,B,C,D,E,F的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
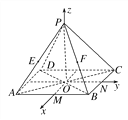
【題目】如圖,已知四棱錐![]() 的底面為矩形,D為
的底面為矩形,D為![]()
的中點,AC⊥平面BCC1B1.
(Ⅰ)證明:AB//平面CDB1;
(Ⅱ)若AC=BC=1,BB1=![]() ,
,
(1)求BD的長;
(2)求三棱錐C-DB1C1的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】成等差數列的三個正數的和等于15,并且這三個數分別加上2、5、13后成為等比數列{bn}中的b3、b4、b5.
(1)求數列{bn}的通項公式;
(2)數列{bn}的前n項和為Sn,求證:數列![]() 是等比數列.
是等比數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2016高考江蘇卷】已知函數![]() .設
.設![]() .
.
(1)求方程![]() 的根;
的根;
(2)若對任意![]() ,不等式
,不等式![]() 恒成立,求實數
恒成立,求實數![]() 的最大值;
的最大值;
(3)若![]() ,函數
,函數![]() 有且只有1個零點,求
有且只有1個零點,求![]() 的值。
的值。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若有窮數列![]() (
(![]() 是正整數),滿足
是正整數),滿足![]() 即
即![]() (
(![]() 是正整數,且
是正整數,且![]() ),就稱該數列為“對稱數列”。例如,數列
),就稱該數列為“對稱數列”。例如,數列![]() 與數列
與數列![]() 都是“對稱數列”.
都是“對稱數列”.
(1)已知數列![]() 是項數為9的對稱數列,且
是項數為9的對稱數列,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 成等差數列,
成等差數列, ![]() ,
, ![]() ,試求
,試求![]() ,
, ![]() ,
, ![]() ,
, ![]() ,并求前9項和
,并求前9項和![]() .
.
(2)若![]() 是項數為
是項數為![]() 的對稱數列,且
的對稱數列,且![]() 構成首項為31,公差為
構成首項為31,公差為![]() 的等差數列,數列
的等差數列,數列![]() 前
前![]() 項和為
項和為![]() ,則當
,則當![]() 為何值時,
為何值時, ![]() 取到最大值?最大值為多少?
取到最大值?最大值為多少?
(3)設![]() 是
是![]() 項的“對稱數列”,其中
項的“對稱數列”,其中![]() 是首項為1,公比為2的等比數列.求
是首項為1,公比為2的等比數列.求![]() 前
前![]() 項的和
項的和![]()
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2017長沙模擬】如圖,在直棱柱ABCA1B1C1中,∠BAC=90°,AB=AC=![]() ,AA1=3,D是BC的中點,點E在棱BB1上運動.
,AA1=3,D是BC的中點,點E在棱BB1上運動.
(1)求證:AD⊥C1E;
(2)當異面直線AC,C1E所成的角為60°時,求三棱錐C1A1B1E的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com