
【題目】已知函數![]() .
.
(1)討論函數![]() 的單調性;
的單調性;
(2)![]() 時, 有
時, 有![]() 恒成立, 求整數
恒成立, 求整數![]() 最小值.
最小值.
 暑假銜接教材期末暑假預習武漢出版社系列答案
暑假銜接教材期末暑假預習武漢出版社系列答案 假期作業暑假成長樂園新疆青少年出版社系列答案
假期作業暑假成長樂園新疆青少年出版社系列答案科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,點
,點![]() 在橢圓
在橢圓![]() 上.
上.
(I)求橢圓![]() 的方程;
的方程;
(II)設動直線![]() 與橢圓
與橢圓![]() 有且僅有一個公共點,判斷是否存在以原點
有且僅有一個公共點,判斷是否存在以原點![]() 為圓心的圓,滿足此圓與
為圓心的圓,滿足此圓與![]() 相交于兩點
相交于兩點![]() (兩點均不在坐標軸上),且使得直線
(兩點均不在坐標軸上),且使得直線![]() 的斜率之積為定值?若存在,求此圓的方程;若不存在,說明理由.
的斜率之積為定值?若存在,求此圓的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】![]() 公司從某大學招收畢業生,經過綜合測試,錄用了
公司從某大學招收畢業生,經過綜合測試,錄用了![]() 名男生和
名男生和![]() 名女生,這
名女生,這![]() 名畢業生的測試成績如莖葉圖所示(單位:分),公司規定:成績在
名畢業生的測試成績如莖葉圖所示(單位:分),公司規定:成績在![]() 分以上者到甲部門工作;
分以上者到甲部門工作;![]() 分以下者到乙部門工作,另外只有成績高于
分以下者到乙部門工作,另外只有成績高于![]() 分才能擔任助理工作。
分才能擔任助理工作。
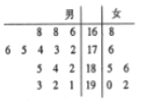
(1)如果用分層抽樣的方法從甲部門人選和乙部門人選中選取![]() 人,再從這
人,再從這![]() 人中選
人中選![]() 人,那么至少有一人是甲部門人選的概率是多少?
人,那么至少有一人是甲部門人選的概率是多少?
(2)若從所有甲部門人選中隨機選![]() 人,用
人,用![]() 表示所選人員中能擔任助理工作的男生人數,寫出
表示所選人員中能擔任助理工作的男生人數,寫出![]() 的分布列,并求出
的分布列,并求出![]() 的數學期望.
的數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了在夏季降溫和冬季供暖時減少能源損耗,房屋的房頂和外墻需要建造隔熱層.某幢建筑物要建造可使用20年的隔熱層,每厘米厚的隔熱層建造成本為6萬元.該建筑物每年的能源消耗費用![]() (單位:萬元)與隔熱層厚度
(單位:萬元)與隔熱層厚度![]() (單位:cm)滿足關系
(單位:cm)滿足關系![]() ,若不建隔熱層,每年能源消耗費用為8萬元,設
,若不建隔熱層,每年能源消耗費用為8萬元,設![]() 為隔熱層建造費用與20年的能源消耗費用之和.
為隔熱層建造費用與20年的能源消耗費用之和.
(1)求![]() 的值及
的值及![]() 的表達式;
的表達式;
(2)隔熱層修建多厚時,總費用![]() 達到最小,并求最小值.
達到最小,并求最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是公差為3的等差數列,數列{bn}滿足b1=1,b2=![]() ,anbn+1+bn+1=nbn.
,anbn+1+bn+1=nbn.
(Ⅰ)分別求數列{an},{bn}的通項公式;
(Ⅱ)令cn= an bn,求數列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】隨機詢問某大學40名不同性別的大學生在購買食物時是否讀營養說明,得到如下列聯表:
性別與讀營養說明列聯表:
男 | 女 | 總計 | |
讀營養說明 | 16 | 8 | 24 |
不讀營養說明 | 4 | 12 | 16 |
總計 | 20 | 20 | 40 |
(Ⅰ)根據以上列聯表進行獨立性檢驗,能否在犯錯誤的概率不超過0.01的前提下認為性別與是否讀營養說明之間有關系?
(Ⅱ)從被詢問的16名不讀營養說明的大學生中,隨機抽取2名學生,求抽到男生人數![]() 的分布列及其均值(即數學期望).
的分布列及其均值(即數學期望).
(注:![]() ,其中
,其中![]() 為樣本容量.)
為樣本容量.)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 的前
的前![]() 項和為
項和為![]() ,
,![]() ,
,![]() 是6與
是6與![]() 的等差中項
的等差中項![]() .
.
(1)求數列![]() 的通項公式;
的通項公式;
(2)是否存在正整數![]() ,使不等式
,使不等式![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的最大值;若不存在,請說明理由.
的最大值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com