
【題目】“冰桶挑戰賽”是一項社交網絡上發起的慈善公益活動,活動規定:被邀請者要么在24小時內接受挑戰,要么選擇為慈善機構捐款(不接受挑戰),并且不能重復參加該活動.若被邀請者接受挑戰,則他需在網絡上發布自己被冰水澆遍全身的視頻內容,然后便可以邀請另外3個人參與這項活動.假設每個人接受挑戰和不接受挑戰是等可能的,且互不影響.
(1)若某參與者接受挑戰后,對其他3個人發出邀請,則這3個人中至少有2個人接受挑戰的概率是多少?
(2)為了解冰桶挑戰賽與受邀者的性別是否有關,某調查機構進行了隨機抽樣調查,調查得到如下![]() 列聯表:
列聯表:
性別 成績 | 接受挑戰 | 不接受挑戰 | 總計 |
男性 | 45 | 15 | 60 |
女性 | 25 | 15 | 40 |
總計 | 70 | 30 | 100 |
根據表中數據,能有有90%的把握認為“冰桶挑戰賽與受邀者的性別有關”?
附:![]() ,其中
,其中![]() .
.
| 2.706 | 3.841 | 6.635 | 10.828 |
| 0.10 | 0.05 | 0.010 | 0.001 |
科目:高中數學 來源: 題型:
【題目】設函數f(x)=(x﹣1)ex﹣kx2(k∈R).
(1)當k=1時,求函數f(x)的單調區間;
(2)當 ![]() 時,求函數f(x)在[0,k]上的最大值M.
時,求函數f(x)在[0,k]上的最大值M.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】當x∈R,|x|<1時,有如下表達式:1+x+x2+…+xn+…= ![]()
兩邊同時積分得: ![]() dx+
dx+ ![]() xdx+
xdx+ ![]() x2dx+…+
x2dx+…+ ![]() xndx+…=
xndx+…= ![]()
![]() dx
dx
從而得到如下等式:1× ![]() +
+ ![]() ×(
×( ![]() )2+
)2+ ![]() ×(
×( ![]() )3+…+
)3+…+ ![]() ×(
×( ![]() )n+1+…=ln2
)n+1+…=ln2
請根據以上材料所蘊含的數學思想方法,計算:![]() ×
× ![]() +
+ ![]()
![]() ×(
×( ![]() )2+
)2+ ![]()
![]() ×(
×( ![]() )3+…+
)3+…+ ![]()
![]() ×(
×( ![]() )n+1= .
)n+1= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司針對企業職工推出一款意外險產品,每年每人只要交少量保費,發生意外后可一次性獲賠50萬元.保險公司把職工從事的所有崗位共分為![]() 、
、![]() 、
、![]() 三類工種,根據歷史數據統計出三類工種的每賠付頻率如下表(并以此估計賠付概率).
三類工種,根據歷史數據統計出三類工種的每賠付頻率如下表(并以此估計賠付概率).


(Ⅰ)根據規定,該產品各工種保單的期望利潤都不得超過保費的20%,試分別確定各類工種每張保單保費的上限;
(Ⅱ)某企業共有職工20000人,從事三類工種的人數分布比例如圖,老板準備為全體職工每人購買一份此種保險,并以(Ⅰ)中計算的各類保險上限購買,試估計保險公司在這宗交易中的期望利潤.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列說法:①用 刻畫回歸效果,當
刻畫回歸效果,當![]() 越大時,模型的擬合效果越差,反之則越好;②歸納推理是由特殊到一般的推理,而演繹推移則是由一般到特殊的推理;③綜合法證明數學問題是“由因索果”,分析法證明數學問題是“執果索因”;④設有一個回歸方程
越大時,模型的擬合效果越差,反之則越好;②歸納推理是由特殊到一般的推理,而演繹推移則是由一般到特殊的推理;③綜合法證明數學問題是“由因索果”,分析法證明數學問題是“執果索因”;④設有一個回歸方程![]() ,變量
,變量![]() 增加1個單位時,
增加1個單位時,![]() 平均增加5個單位;⑤線性回歸方程
平均增加5個單位;⑤線性回歸方程![]() 必過點
必過點![]() .其中錯誤的個數有( )
.其中錯誤的個數有( )
A. 0個 B. 1個 C. 2個 D. 3個
查看答案和解析>>
科目:高中數學 來源: 題型:
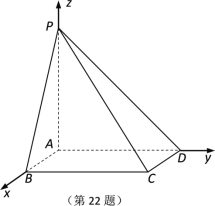
【題目】如圖所示,在四棱錐![]() 中,底面
中,底面![]() 是矩形,
是矩形,![]() 平面
平面![]() ,AB 1,AP AD 2.
,AB 1,AP AD 2.
(1)求直線![]() 與平面
與平面![]() 所成角的正弦值;
所成角的正弦值;
(2)若點M,N分別在AB,PC上,且![]() 平面
平面![]() ,試確定點M,N的位置.
,試確定點M,N的位置.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現采用隨機模擬的方法估計某運動員射擊4次,至少擊中3次的概率:先由計算器給出0到9之間取整數值的隨機數,指定0,1表示沒有擊中目標,2,3,4,5,6,7,8,
9表示擊中目標,以4個隨機數為一組,代表射擊4次的結果,經隨機模擬產生了20組隨機數:
7527 | 0293 | 7140 | 9857 | 0347 | 4373 | 8636 | 6947 | 1417 | 4698 |
0371 | 6233 | 2616 | 8045 | 6011 | 3661 | 9597 | 7424 | 7610 | 4281 |
根據以上數據估計該射擊運動員射擊4次至少擊中3次的概率為_______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設f(x)=alnx+ ![]() +
+ ![]() x+1,其中a∈R,曲線y=f(x)在點(1,f(1))處的切線垂直于y軸.
x+1,其中a∈R,曲線y=f(x)在點(1,f(1))處的切線垂直于y軸.
(1)求a的值;
(2)求函數f(x)的極值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com