
【題目】設直線![]() 與直線
與直線![]() 分別與橢圓
分別與橢圓![]()
![]() 交于點
交于點![]() ,且四邊形
,且四邊形![]() 的面積為
的面積為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)設過點![]() 的動直線
的動直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() ,
,![]() 兩點,是否存在經過原點,且以
兩點,是否存在經過原點,且以![]() 為直徑的圓?若有,請求出圓的方程,若沒有,請說明理由.
為直徑的圓?若有,請求出圓的方程,若沒有,請說明理由.
【答案】(1)![]() ;(2)存在,圓的方程為
;(2)存在,圓的方程為 .
.
【解析】
(1)根據兩條直線解析式特征可知直線![]() 與直線
與直線![]() 關于坐標軸對稱,則
關于坐標軸對稱,則![]() 為矩形,將
為矩形,將![]() 與橢圓方程聯立,表示出交點的橫縱坐標,即可由四邊形
與橢圓方程聯立,表示出交點的橫縱坐標,即可由四邊形![]() 的面積確定參數,求得橢圓
的面積確定參數,求得橢圓![]() 的方程;
的方程;
(2)設直線![]() 的方程
的方程![]() ,兩個交點坐標
,兩個交點坐標![]() .聯立橢圓方程后化簡,用韋達定理表示出
.聯立橢圓方程后化簡,用韋達定理表示出![]() ,經過原點,且以
,經過原點,且以![]() 為直徑的圓滿足
為直徑的圓滿足![]() ,即
,即![]() ,由平面向量數量積的坐標運算代入即可求得斜率
,由平面向量數量積的坐標運算代入即可求得斜率![]() .由中點坐標公式即可求得線段
.由中點坐標公式即可求得線段![]() 中點
中點![]() 的坐標,進而求得
的坐標,進而求得![]() 的值,即可得圓的標準方程.
的值,即可得圓的標準方程.
(1)由題意可知直線![]() 與直線
與直線![]() 關于坐標軸對稱,所以四邊形
關于坐標軸對稱,所以四邊形![]() 為矩形,
為矩形,
則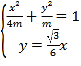 ,解得
,解得![]()
所以![]() ,
,
解得![]() ,
,
代入橢圓方程可得![]() .
.
(2)存在.
設![]() ,由題意可知直線
,由題意可知直線![]() 的斜率必然存在.
的斜率必然存在.
直線![]() 過點
過點![]() ,設直線
,設直線![]() 的方程為
的方程為![]() ,
,
則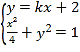 ,化簡可得
,化簡可得![]() ,
,
所以![]() ,
,
經過原點,且以![]() 為直徑的圓滿足
為直徑的圓滿足![]() ,即
,即![]() ,
,
則![]()
![]()
![]()
![]()
![]() ,
,
解方程可得![]() ,經檢驗可知都滿足
,經檢驗可知都滿足![]() .
.
設線段![]() 的中點為
的中點為![]() .
.
則![]()
![]()
所以![]() ,
,
所以存在滿足條件的圓,圓的方程為 .
.


科目:高中數學 來源: 題型:
【題目】過拋物線C:x2=4y的準線上任意一點P作拋物線的切線PA,PB,切點分別為A,B,則A點到準線的距離與B點到準線的距離之和的最小值是( )
A.7B.6C.5D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的質量以其質量指標值衡量,并依據質量指標值劃分等級如表:
質量指標值m | 25≤m<35 | 15≤m<25或35≤m<45 | 0<m<15或45≤m<65 |
等級 | 一等品 | 二等品 | 三等品 |
某企業從生產的這種產品中抽取100件產品作為樣本,檢測其質量指標值,得到下圖的率分布直方圖.(同一組數據用該區間的中點值作代表)
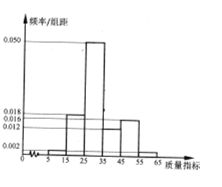
(1)該企業為提高產品質量,開展了質量提升月”活動,活動后再抽樣檢測,產品三等品數Y近似滿足Y~H(10,15,100),請測算“質量提升月”活動后這種產品的“二等品率“(一、二等品其占全部產品百分比)較活動前提高多少個百分點?
(2)若企業每件一等品售價180元,每件二等品售價150元,每件三等品售價120元,以樣本中的頻率代替相應概率,現有一名聯客隨機購買兩件產品,設其支付的費用為X(單位:元),求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】中國古代儒家要求學生掌握六種基本才藝:禮、樂、射、御、書、數,簡稱“六藝”,某高中學校為弘揚“六藝”的傳統文化,分別進行了主題為“禮、樂、射、御、書、數”六場傳統文化知識競賽,現有甲、乙、丙三位選手進入了前三名的最后角逐,規定:每場知識競賽前三名的得分都分別為![]()
![]() 且
且![]() ;選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為
;選手最后得分為各場得分之和,在六場比賽后,已知甲最后得分為![]() 分,乙和丙最后得分都是
分,乙和丙最后得分都是![]() 分,且乙在其中一場比賽中獲得第一名,下列說法正確的是( )
分,且乙在其中一場比賽中獲得第一名,下列說法正確的是( )
A. 乙有四場比賽獲得第三名
B. 每場比賽第一名得分![]() 為
為![]()
C. 甲可能有一場比賽獲得第二名
D. 丙可能有一場比賽獲得第一名
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年是五四運動100周年.五四運動以來的100年,是中國青年一代又一代接續奮斗、凱歌前行的100年,是中口青年用青春之我創造青春之中國、青春之民族的100年.為繼承和發揚五四精神在青年節到來之際,學校組織“五四運動100周年”知識競賽,競賽的一個環節由10道題目組成,其中6道A類題、4道B類題,參賽者需從10道題目中隨機抽取3道作答,現有甲同學參加該環節的比賽.
(1)求甲同學至少抽到2道B類題的概率;
(2)若甲同學答對每道A類題的概率都是![]() ,答對每道B類題的概率都是
,答對每道B類題的概率都是![]() ,且各題答對與否相互獨立.現已知甲同學恰好抽中2道A類題和1道B類題,用X表示甲同學答對題目的個數,求隨機變量X的分布列和數學期望.
,且各題答對與否相互獨立.現已知甲同學恰好抽中2道A類題和1道B類題,用X表示甲同學答對題目的個數,求隨機變量X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某區“創文明城區”(簡稱“創城”)活動中,教委對本區![]() 四所高中學校按各校人數分層抽樣,隨機抽查了100人,將調查情況進行整理后制成下表:
四所高中學校按各校人數分層抽樣,隨機抽查了100人,將調查情況進行整理后制成下表:
學校 |
|
|
|
|
抽查人數 | 50 | 15 | 10 | 25 |
“創城”活動中參與的人數 | 40 | 10 | 9 | 15 |
(注:參與率是指:一所學校“創城”活動中參與的人數與被抽查人數的比值)假設每名高中學生是否參與”創城”活動是相互獨立的.
(1)若該區共2000名高中學生,估計![]() 學校參與“創城”活動的人數;
學校參與“創城”活動的人數;
(2)在隨機抽查的100名高中學生中,隨機抽取1名學生,求恰好該生沒有參與“創城”活動的概率;
(3)在上表中從![]() 兩校沒有參與“創城”活動的同學中隨機抽取2人,求恰好
兩校沒有參與“創城”活動的同學中隨機抽取2人,求恰好![]() 兩校各有1人沒有參與“創城”活動的概率是多少?
兩校各有1人沒有參與“創城”活動的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】甲、乙兩支籃球隊賽季總決賽采用7場4勝制,每場必須分出勝負,場與場之間互不影響,只要有一隊獲勝4場就結束比賽.現已比賽了4場,且甲籃球隊勝3場.已知甲球隊第5,6場獲勝的概率均為![]() ,但由于體力原因,第7場獲勝的概率為
,但由于體力原因,第7場獲勝的概率為![]() .
.
(1)求甲隊分別以![]() ,
,![]() 獲勝的概率;
獲勝的概率;
(2)設![]() 表示決出冠軍時比賽的場數,求
表示決出冠軍時比賽的場數,求![]() 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若采用隨機模擬的方法估計某運動員射擊擊中目標的概率.先由計算器給出0到9之間取整數的隨機數,指定0,1,2,3表示沒有擊中目標,4,5,6,7,8,9表示擊中目標,以4個隨機數為一組,代表射擊4次的結果,經隨機模擬產生了20組如下的隨機數:
7327 0293 7140 9857 0347 4373 8636 6947 1417 4698
0371 6233 2616 8045 6011 3661 9597 7424 7610 4281
根據以上數據估計該運動員射擊4次至少擊中3次的概率為__________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com