
如圖,點 是以線段
是以線段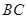 為直徑的圓
為直徑的圓 上一點,
上一點,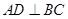 于點
于點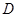 ,過點
,過點 作圓
作圓 的切線,與
的切線,與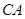 的延長線交于點
的延長線交于點 ,點
,點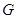 是
是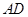 的中點,連結(jié)
的中點,連結(jié)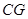 并延長與
并延長與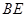 相交于點
相交于點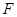 ,延長
,延長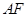 與
與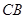 的延長線相交于點
的延長線相交于點 .
.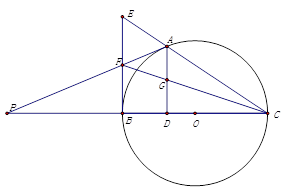
(Ⅰ)求證: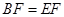 ;
;
(Ⅱ)求證: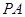 是圓
是圓 的切線.
的切線.
(Ⅰ)詳見試題解析;(Ⅱ)詳見試題解析.
解析試題分析:(Ⅰ)由 ,
,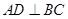 可得
可得 ,從而可得
,從而可得
通過等量代換及題設(shè)“點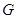 是
是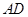 的中點”可得
的中點”可得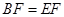 .
.
(Ⅱ)目標是要證 是直角,連結(jié)
是直角,連結(jié) 便可看出只要證得
便可看出只要證得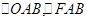 是等腰三角形即可.
是等腰三角形即可.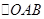 顯然是等腰三角形。因為直徑上的圓周角是直角,
顯然是等腰三角形。因為直徑上的圓周角是直角, ,所以
,所以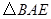 是直角三角形. 由(Ⅰ)得
是直角三角形. 由(Ⅰ)得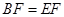 所以
所以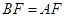 ,從而本題得證.
,從而本題得證.
試題解析:證明:(Ⅰ) 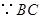 是圓
是圓 的直徑,
的直徑,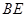 是圓
是圓 的切線,
的切線, .又
.又 ,
, .
.
可以得知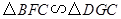 ,
,  .
. .
.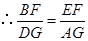 .
.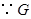 是
是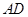 的中點,
的中點, .
.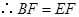 . 5分
. 5分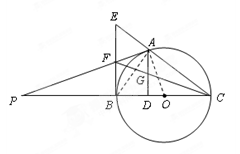
(Ⅱ)連結(jié) .
.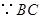 是圓
是圓 的直徑,
的直徑, .
.
在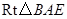 中,由(Ⅰ)得知
中,由(Ⅰ)得知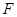 是斜邊
是斜邊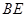 的中點,
的中點, .
. .
.
又 ,
, .
.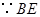 是圓
是圓 的切線,
的切線,
 ,
, 是圓
是圓 的切線. 10分
的切線. 10分
考點:1、相似三角形;2、圓的性質(zhì);3、等量代換;4、直角三角形斜邊上的中線;5、幾何證明


 課時訓(xùn)練江蘇人民出版社系列答案
課時訓(xùn)練江蘇人民出版社系列答案 黃岡經(jīng)典趣味課堂系列答案
黃岡經(jīng)典趣味課堂系列答案 啟東小題作業(yè)本系列答案
啟東小題作業(yè)本系列答案科目:高中數(shù)學 來源: 題型:解答題
(拓展深化)如圖,已知△ABC中的兩條角平分線AD和CE相交于H,∠B=60°,F(xiàn)在AC上,且AE=AF.
(1)證明:B、D、H、E四點共圓;
(2)證明:CE平分∠DEF.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖,直線AB經(jīng)過⊙O上的點C,并且OA=OB,CA=CB,⊙O交直線OB于E、D,連結(jié)EC、CD.
(Ⅰ)求證:直線AB是⊙O的切線;
(Ⅱ)若tan∠CED= ,⊙O的半徑為3,求OA的長.
,⊙O的半徑為3,求OA的長.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖,已知⊙O的半徑為1,MN是⊙O的直徑,過M點作⊙O的切線AM,C是AM的中點,AN交⊙O于B點,若四邊形BCON是平行四邊形.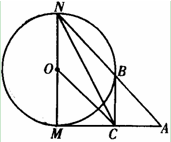
(Ⅰ)求AM的長;
(Ⅱ)求sin∠ANC.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖AB為圓O直徑,P為圓O外一點,過P點作PC⊥AB,
垂是為C,PC交圓O于D點,PA交圓O于E點,BE交PC于F點。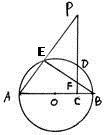
(I)求證:∠PFE=∠PAB;
(II)求證:CD2=CF·CP.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com