
| 3 |
| m |
| 3 |
| lim |
| n→∞ |
| (-2)n-3n |
| 3n+2n |
| 1 |
| n(n+2) |
| 3 |
| 4 |
| 1 |
| 2 |
| 2x+1 |
| x-1 |
| 3 |
| m |
| 3 |
| 3 |
| m |
| 3 |
| 3 |
| lim |
| n→∞ |
| (-2)n-3n |
| 3n+2n |
| lim |
| n→∞ |
(-
| ||
1+(
|
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 2n+3 |
| n2+3n+2 |
| lim |
| n→∞ |
| lim |
| n→∞ |
| 3 |
| 4 |
| 1 |
| 2 |
| 2n+3 |
| n2+3n+2 |
| 3 |
| 4 |
| 2x+1 |
| x-1 |
| 3 |
| m |
| 3 |
| 3 |
| m |
| 3 |
| 3 |
| lim |
| n→∞ |
| (-2)n-3n |
| 3n+2n |
| lim |
| n→∞ |
(-
| ||
1+(
|
| 1 |
| n(n+2) |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2 |
| 1 |
| n |
| 1 |
| n+2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 3 |
| 4 |
| 1 |
| 2 |
| 2n+3 |
| n2+3n+2 |
| lim |
| n→∞ |
| lim |
| n→∞ |
| 3 |
| 4 |
| 1 |
| 2 |
| 2n+3 |
| n2+3n+2 |
| 3 |
| 4 |
| 2x+1 |
| x-1 |


 陽光課堂課時優(yōu)化作業(yè)系列答案
陽光課堂課時優(yōu)化作業(yè)系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
| 1 | 4 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:“伴你學(xué)”新課程 數(shù)學(xué)·選修1-2(人教B版) 人教B版 題型:013
已知m、n是不重合的直線,α、β是不重合的平面,有下列命題:
(1)若m![]() α,n∥α,則m∥n;
α,n∥α,則m∥n;
(2)若m∥α,m∥β,則α∥β;
(3)若α∩β=n,m∥n,則m∥α且m∥β;
(4)若m⊥α,m⊥β,則α∥β.
其中真命題的個數(shù)是
0
1
2
3
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:數(shù)學(xué)教研室 題型:013
已知m、n是兩條不重合的直線,α、β、γ是三個兩兩不重合的平面,給出下列命題:
(1)若m∥β,n∥β且m α,n
α,n α,則α∥β;
α,則α∥β;
(2)若α∩β=n,m∥n,則m∥α且m∥β;
(3)若m⊥α,m∥β,則α⊥β;
(4)若α∥β,且γ∩α=m,γ∩β=n,則m∥n.
其中的正確命題是
[ ]
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:013
已知
m、n是兩條不重合的直線,α、β、γ是三個兩兩不重合的平面,給出下列命題:(1)
若m∥β,n∥β且m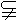 α,n
α,n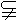 α,則α∥β;
α,則α∥β;
(2)
若α∩β=n,m∥n,則m∥α且m∥β;(3)
若m⊥α,m∥β,則α⊥β;(4)
若α∥β,且γ∩α=m,γ∩β=n,則m∥n.其中的正確命題是
[
]|
A .(1)和(3) |
B .(1)和(4) |
|
C .(2)和(4) |
D .(3)和(4) |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源:2010-2011年四川省成都市高二3月月考數(shù)學(xué)試卷 題型:填空題
已知α,β是平面,m,n是直線. 給出下列命題:
①.若m∥n,m⊥α,則n⊥α ②.若m⊥α,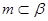 ,則α⊥β
,則α⊥β
③.若m⊥α,m⊥β,則α∥β ④.若m∥α,α∩β=n,則m∥n其中,真命題的編號是_ ▲ (寫出所有正確結(jié)論的編號).
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com