
【題目】已知函數f(x)=![]() (其中e是自然對數的底數,常數a>0).
(其中e是自然對數的底數,常數a>0).
(1)當a=1時,求曲線在(0,f(0))處的切線方程;
(2)若存在實數x∈(a,2],使得不等式f(x)≤e2成立,求a的取值范圍.
【答案】(1)切線方程為![]() .(2)a的取值范圍是(0,1].
.(2)a的取值范圍是(0,1].
【解析】試題分析:(1)根據導數幾何意義得切線斜率,再根據點斜式求切線方程(2)先變量分離得![]() ,再利用導數求函數
,再利用導數求函數![]() 最大值,即得a的取值范圍.
最大值,即得a的取值范圍.
試題解析:(1)f(x)的定義域為{x|x≠a}.
當a=1時,f(x)=![]() ,f′(x)=
,f′(x)=![]() ,
,
∴f(0)=-1,f′(0)=-2.
∴曲線在(0,f(0))處的切線方程為
2x+y+1=0.
(2)f′(x)=![]() ,
,
令f′(x)=0,x=a+1,
∴f(x)在(-∞,a),(a,a+1)上遞減,
在(a+1,+∞)上遞增.6分
若存在x∈(a,2],使不等式f(x)≤e2成立,只需在x∈(a,2]上,f(x)min≤e2成立.
①當a+1≤2,即0<a≤1時,f(x)min=f(a+1)=ea+1≤e2,
∴0<a≤1符合條件.10分
②當a+1>2,即1<a<2時,
f(x)min=f(2)=![]() ≤e2,解得a≤1,
≤e2,解得a≤1,
又1<a<2,∴a∈.
綜上,a的取值范圍是(0,1].


 華東師大版一課一練系列答案
華東師大版一課一練系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=(2-a)lnx+![]() +2ax.
+2ax.
(1)當a<0時,討論f(x)的單調性;
(2)若對任意的a∈(-3,-2),x1,x2∈[1,3],恒有(m+ln 3)a-2ln 3>|f(x1)-f(x2)|成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將2張邊長均為1分米的正方形紙片分別按甲、乙兩種方式剪裁并廢棄陰影部分.
(1)在圖甲的方式下,剩余部分恰能完全覆蓋某圓錐的表面,求該圓錐的母線長及底面
半徑;
(2)在圖乙的方式下,剩余部分能完全覆蓋一個長方體的表面,求長方體體積的最大值.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某互聯網理財平臺為增加平臺活躍度決定舉行邀請好友拿獎勵活動,規則是每邀請一位好友在該平臺注冊,并購買至少1萬元的12月定期,邀請人可獲得現金及紅包獎勵,現金獎勵為被邀請人理財金額的![]() ,且每邀請一位最高現金獎勵為300元,紅包獎勵為每邀請一位獎勵50元.假設甲邀請到乙、丙兩人,且乙、丙兩人同意在該平臺注冊,并進行理財,乙、丙兩人分別購買1萬元、2萬元、3萬元的12月定期的概率如下表:
,且每邀請一位最高現金獎勵為300元,紅包獎勵為每邀請一位獎勵50元.假設甲邀請到乙、丙兩人,且乙、丙兩人同意在該平臺注冊,并進行理財,乙、丙兩人分別購買1萬元、2萬元、3萬元的12月定期的概率如下表:
理財金額 |
|
|
|
乙理財相應金額的概率 |
|
|
|
丙理財相應金額的概率 |
|
|
|
(1)求乙、丙理財金額之和不少于5萬元的概率;
(2)若甲獲得獎勵為![]() 元,求
元,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x(1-![]() )是R上的偶函數.
)是R上的偶函數.
(1)對任意的x∈[1,2],不等式m·![]() ≥2x+1恒成立,求實數m的取值范圍.
≥2x+1恒成立,求實數m的取值范圍.
(2)令g(x)=1-![]() ,設函數F(x)=g(4x-n)-g(2x+1-3)有零點,求實數n的取值范圍.
,設函數F(x)=g(4x-n)-g(2x+1-3)有零點,求實數n的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在棱長為1的正方體ABCD-A1B1C1D1中,點P在線段AD1上運動,給出以下命題:

①異面直線C1P與B1C所成的角為定值;
②二面角P-BC1-D的大小為定值;
③三棱錐D-BPC1的體積為定值;
④異面直線A1P與BC1間的距離為定值.
其中真命題的個數為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在梯形ABCD中,AD∥BC,AD⊥DC,BC=2AD,四邊形ABEF是矩形,將矩形ABEF沿AB折起到四邊形ABE1F1的位置,使平面ABE1F1⊥平面ABCD,M為AF1的中點,如圖2.
(1)求證:BE1⊥DC;
(2)求證:DM∥平面BCE1;
(3)判斷直線CD與ME1的位置關系,并說明理由.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】學校從參加安全知識競賽的同學中,選取60名同學將其成績(百分制,均為整數,成績![]() 分記為優秀)分成6組后,得到部分頻率分布直方圖(如圖),觀察圖形中的信息,回答下列問題:
分記為優秀)分成6組后,得到部分頻率分布直方圖(如圖),觀察圖形中的信息,回答下列問題:
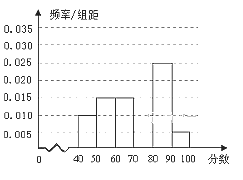
(1)求分數在[70,80)內的頻率,并補全這個頻率分布直方圖;
(2)從頻率分布直方圖中,估計本次考試的平均分;
(3)為參加市里舉辦的安全知識競賽,學校舉辦預選賽.已知在學校安全知識競賽中優秀的同學通過預選賽的概率為![]() ,現在從學校安全知識競賽中優秀的同學中選3人參加預選賽,若隨機變量
,現在從學校安全知識競賽中優秀的同學中選3人參加預選賽,若隨機變量![]() 表示這3人中通過預選賽的人數,求
表示這3人中通過預選賽的人數,求![]() 的分布列與數學期望.
的分布列與數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知f(x)=a(x-lnx)+![]() ,a∈R.
,a∈R.
(I)討論f(x)的單調性;
(II)當a=1時,證明f(x)>f’(x)+![]() 對于任意的x∈[1,2] 恒成立。
對于任意的x∈[1,2] 恒成立。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com