
已知函數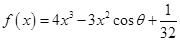 ,其中
,其中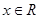 ,
,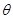 為參數,且
為參數,且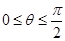 .
.
(1)當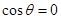 時,判斷函數
時,判斷函數 是否有極值;
是否有極值;
(2)要使函數 的極小值大于零,求參數
的極小值大于零,求參數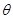 的取值范圍;
的取值范圍;
(3)若對(2)中所求的取值范圍內的任意參數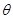 ,函數
,函數 在區間
在區間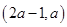 內都是增函數,求實數
內都是增函數,求實數 的取值范圍.
的取值范圍.
(1) 無極值;(2)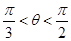 ;(3)
;(3) .
.
解析試題分析:(1) 當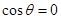 時,
時, ,利用函數單調性的定義或導數法可證明
,利用函數單調性的定義或導數法可證明 在
在 內是增函數,故無極值;(2)先求函數
內是增函數,故無極值;(2)先求函數 的導數:
的導數: ,令
,令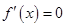 ,得可能的極值點:
,得可能的極值點: .由
.由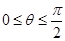 及(1),只需考慮
及(1),只需考慮 的情況,列表考慮當
的情況,列表考慮當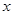 變化時,
變化時, 的符號及
的符號及 的變化情況,求得函數
的變化情況,求得函數 的極小值,最后根據題意列極小值大于零的不等式,解不等式求出參數
的極小值,最后根據題意列極小值大于零的不等式,解不等式求出參數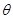 的取值范圍;(3)由(2)知,函數
的取值范圍;(3)由(2)知,函數 在區間
在區間 與
與 內都是增函數.由題設,函數
內都是增函數.由題設,函數 在
在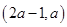 內是增函數,因而
內是增函數,因而 必須滿足不等式組
必須滿足不等式組 或
或 進而可求得
進而可求得 的取值范圍.
的取值范圍.
試題解析:(1)當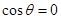 時,
時, ,則
,則 在
在 內是增函數,故無極值.
內是增函數,故無極值.
(2) ,令
,令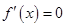 ,得
,得 .由
.由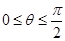 及(1),只需考慮
及(1),只需考慮 的情況.當
的情況.當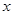 變化時,
變化時, 的符號及
的符號及 的變化情況如下表:
的變化情況如下表: