
【題目】為了治療某種疾病,某科研機構研制了甲、乙兩種新藥,為此進行白鼠試驗.試驗方案如下:每一輪選取兩只白鼠對藥效進行對比試驗.對于兩只白鼠,隨機選一只施以甲藥,另一只施以乙藥一輪的治療結果得出后,再安排下一輪試驗.4輪試驗后,就停止試驗.甲、乙兩種藥的治愈率分別是![]() 和
和![]() .
.
(1)若![]() ,求2輪試驗后乙藥治愈的白鼠比甲藥治愈的白鼠多1只的概率;
,求2輪試驗后乙藥治愈的白鼠比甲藥治愈的白鼠多1只的概率;
(2)已知A公司打算投資甲、乙這兩種新藥的試驗耗材費用,甲藥和乙藥一次試驗耗材花費分別為3千元和![]() 千元,每輪試驗若甲、乙兩種藥都治愈或都沒有治愈,則該科研機構和A公司各承擔該輪試驗耗材總費用的50%;若甲藥治愈,乙藥未治愈,則A公司承擔該輪試驗耗材總費用的75%,其余由科研機構承擔,若甲藥未治愈,乙藥治愈,則A公司承擔該輪試驗耗材總費用的25%,其余由科研機構承擔.以A公司每輪支付試驗耗材費用的期望為標準,求A公司4輪試驗結束后支付試驗耗材最少費用為多少元?
千元,每輪試驗若甲、乙兩種藥都治愈或都沒有治愈,則該科研機構和A公司各承擔該輪試驗耗材總費用的50%;若甲藥治愈,乙藥未治愈,則A公司承擔該輪試驗耗材總費用的75%,其余由科研機構承擔,若甲藥未治愈,乙藥治愈,則A公司承擔該輪試驗耗材總費用的25%,其余由科研機構承擔.以A公司每輪支付試驗耗材費用的期望為標準,求A公司4輪試驗結束后支付試驗耗材最少費用為多少元?
【答案】(1)![]() ;(2)14400元.
;(2)14400元.
【解析】
(1)利用和事件的概率公式、獨立事件的概率公式,結合獨立重復試驗概率公式進行求解即可;
(2)設隨機變量X為每輪試驗A公司需要支付的試驗耗材費用的取值,根據題意求出隨機變量X的可能取值,以及相應的概率,列出分布列,計算數學期望,最后利用二次函數的單調性進行求解即可.
解析:(1)記事件A為“2輪試驗后,乙藥治愈的白鼠比甲藥治愈的白鼠多1只”,
事件B為“2輪試驗后,乙藥治愈1只白鼠,甲藥治愈0只白鼠”,
事件C為“2輪試驗后,乙藥治愈2只白鼠,甲藥治愈1只白鼠”,
則![]() ,
,
![]() ,
,
![]()
(2)一次實驗耗材總費用為![]() 千元.
千元.
設隨機變量X為每輪試驗A公司需要支付的試驗耗材費用的取值,
則![]() ,
,![]() ,
,![]()
![]() ,
,
![]() ,
,
![]() .
.
X |
|
|
|
P |
|
|
|
![]()
![]()
令![]() ,
,![]() .
.
函數![]() 的對稱軸為:
的對稱軸為:![]() ,所以
,所以![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
∴![]() (千元).
(千元).
則A公司4輪試驗結束后支付實驗耗材最少費用為![]() (千元),
(千元),
即14400元.


科目:高中數學 來源: 題型:
【題目】已知函數![]()
(1)當a=-2時,求函數f(x)的極值;
(2)若ln[e(x+1)]≥2- f(-x)對任意的x∈[0,+∞)成立,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線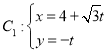 (t為參數),曲線
(t為參數),曲線![]() ,(
,(![]() 為參數),以坐標原點O為極點,x軸正半軸為極軸,建立極坐標系.
為參數),以坐標原點O為極點,x軸正半軸為極軸,建立極坐標系.
(1)求曲線![]() ,
,![]() 的極坐標方程;
的極坐標方程;
(2)射線![]() 分別交
分別交![]() ,
,![]() 于A,B兩點,求
于A,B兩點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若存在實常數![]() 和
和![]() ,使得函數
,使得函數![]() 和
和![]() 對其公共定義域上的任意實數x都滿足:
對其公共定義域上的任意實數x都滿足:![]() 和
和![]() 恒成立,則稱此直線
恒成立,則稱此直線![]() 為
為![]() 和
和![]() 的“隔離直線”,已知函數
的“隔離直線”,已知函數![]() ,
,![]() ,
,![]() (
(![]() 為自然對數的底數),則( )
為自然對數的底數),則( )
A.![]() 在
在![]() 內單調遞增;
內單調遞增;
B.![]() 和
和![]() 之間存在“隔離直線”,且
之間存在“隔離直線”,且![]() 的最小值為
的最小值為![]() ;
;
C.![]() 和
和![]() 之間存在“隔離直線”,且
之間存在“隔離直線”,且![]() 的取值范圍是
的取值范圍是![]() ;
;
D.![]() 和
和![]() 之間存在唯一的“隔離直線”
之間存在唯一的“隔離直線”![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】垃圾分類是對垃圾進行有效處置的一種科學管理方法.太原市為推進這項工作的實施,開展了“垃圾分類進小區”的評比活動.現有甲、乙兩個小區采取不同的宣傳與倡導方式對各自小區居民進行了有關垃圾分類知識的培訓,并參加了評比活動,評委會隨機從兩個小區各選出20戶家庭進行評比打分,每戶成績滿分為100分,評分后得到如下莖葉圖.
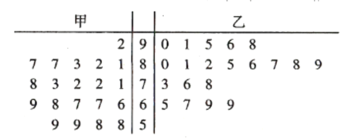
(1)依莖葉圖判斷哪個小區的平均分高?
(2)現從甲小區不低于80分的家庭中隨機抽取兩戶,求分數為87的家庭至少有一戶被抽中的概率;
(3)如果規定分數不低于85分的家庭為優秀,請填寫下面的![]() 列聯表,并判斷“能否在犯錯誤的概率不超過0.025的前提下認為得分是否優秀與小區宣傳培訓方式有關?”
列聯表,并判斷“能否在犯錯誤的概率不超過0.025的前提下認為得分是否優秀與小區宣傳培訓方式有關?”
甲 | 乙 | 合計 | |
優秀 |
|
| |
不優秀 |
|
| |
合計 |
參考公式和數據: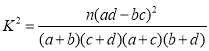 ,其中
,其中![]() .
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某同學對函數![]() 進行研究后,得出以下結論,其中正確的有( )
進行研究后,得出以下結論,其中正確的有( )
A.函數![]() 的圖象關于原點對稱
的圖象關于原點對稱
B.對定義域中的任意實數![]() 的值,恒有
的值,恒有![]() 成立
成立
C.函數![]() 的圖象與
的圖象與![]() 軸有無窮多個交點,且每相鄰兩交點間距離相等
軸有無窮多個交點,且每相鄰兩交點間距離相等
D.對任意常數![]() ,存在常數
,存在常數![]() ,使函數
,使函數![]() 在
在![]() 上單調遞減,且
上單調遞減,且![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正方體![]() 棱長為
棱長為![]() ,如圖,
,如圖,![]() 為
為![]() 上的動點,
上的動點,![]() 平面
平面![]() .下面說法正確的是( )
.下面說法正確的是( )
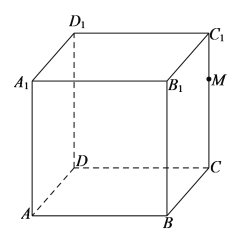
A.直線![]() 與平面
與平面![]() 所成角的正弦值范圍為
所成角的正弦值范圍為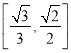
B.點![]() 與點
與點![]() 重合時,平面
重合時,平面![]() 截正方體所得的截面,其面積越大,周長就越大
截正方體所得的截面,其面積越大,周長就越大
C.點![]() 為
為![]() 的中點時,若平面
的中點時,若平面![]() 經過點
經過點![]() ,則平面
,則平面![]() 截正方體所得截面圖形是等腰梯形
截正方體所得截面圖形是等腰梯形
D.己知![]() 為
為![]() 中點,當
中點,當![]() 的和最小時,
的和最小時,![]() 為
為![]() 的中點
的中點
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com